After saving enough money to retire, Bảo has accumulated a considerable amount and decided to build a new ecological garden. With his rich imagination, Bảo designed the garden to include ~n~ small gardens with the following details:

• Each garden ~i~ is circular and surrounded by a wall. On the wall, there are ~c~ evenly spaced doors. Note: all gardens have the same number of doors.

• For garden ~i~, there are ~m_i~ flower paths (chords). The ~j~-th path of the garden ~i~ connects two doors ~u_j, v_j~ and crosses the internal passage of that garden.

• Tourists who want to go straight from door ~x~ to door ~y~ within the same garden must jump over all the flower paths that intersect the straight line connecting those two doors(refer to the illustration below)

  

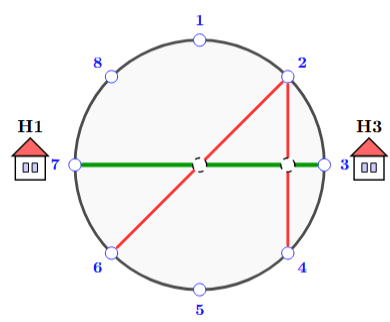
  The visitor's path from door ~7~ to door ~3~, crossing two red flower paths ~(2, 4)~ and ~(2, 6)~

• Outside the wall, the gardens are connected by ~n - 1~ paths. This path system ensures that there is always a way back and forth between any two gardens. The ~k~-th path connects door ~u_k~ of garden ~x_k~ to door ~v_k~ of garden ~y_k~.

• Each door can only be used for one purpose. If a door is connected to an outside path, it cannot be connected to an internal flower path, and vice versa.

Noticing that visitors move with great difficulty in this design, Bảo added ~d~ rest houses scattered throughout the tourist area. The rest houss ~t~ placed right behind door ~u_t~ of any garden ~x_t~. The position of the rest house also follows the above rule: a door that has a rest house cannot be connected to any other path or flower path.

To evaluate the quality of the design, the "inconvenience score" between any two rest houses ~u~ and ~v~ is calculated by the total number of flower paths that need to be jumped over when traveling from one rest house to the other. To assess this comprehensively, Bảo wonders what the total inconvenience score of all pairs of rest houses in this garden is. Please help Bảo!

Input

The first line contains a positive integer ~T~ — the number of test cases.

Each test case is described as follows:

• The first line contains 3 positive integers ~n, d, c~ (~1 \le n, d \le 2 \times 10^5~, ~1 \le c \le 10^9~) — the number of gardens, rest houses, and the number of doors in each garden.

• The next ~n~ groups of the data contain information about each garden:

  • The first line contains a positive integer ~m_i~ (~1 \leq m_i \leq 2 \times 10^5~) — the number of doors and flower paths in the ~i~-th garden.

  • The ~i~-th of the next ~m_i~ lines each contain three positive integers ~u_j, v_j~ (~1 \leq u_j, v_j \leq c~) — a flower path connecting the ~u_j~-th and ~v_j~-th doors.

• The ~k~-th of the next ~n - 1~ lines contain five positive integers ~x_k, u_k, y_k, v_k~ (~1 \leq x_k, y_k \leq n, 1 \leq u_k, v_k \leq c~) — the path connecting door ~u_k~ of garden ~x_k~ to door ~v_k~ of garden ~y_k~.

• The ~t~-th of the last ~d~ lines contain two positive integers ~x_t, u_t~ (~1 \leq x_t \leq n, 1 \leq u_t \leq c~) — the position of the ~t~-th rest house.

• The data guarantees that each door is connected to at most one flower path, outside path, or rest house.

It is guaranteed that across all test cases, the total of ~\sum n~ and ~\sum d~ does not exceed ~2 \times 10^5~ respectively, and the total ~\sum m_i~ does not exceed ~6 \times 10^5~.

Output

For each test case, output a single integer — the total inconvenience score between the rest houses.

Sample Input 1

1
4 3 8
2
2 4
2 6
0
0
1
2 4
1 3 4 1
1 5 2 1
1 7 3 1
2 2
3 2
4 3

Sample Output 1

6

Notes

The image illustrates the example test case.

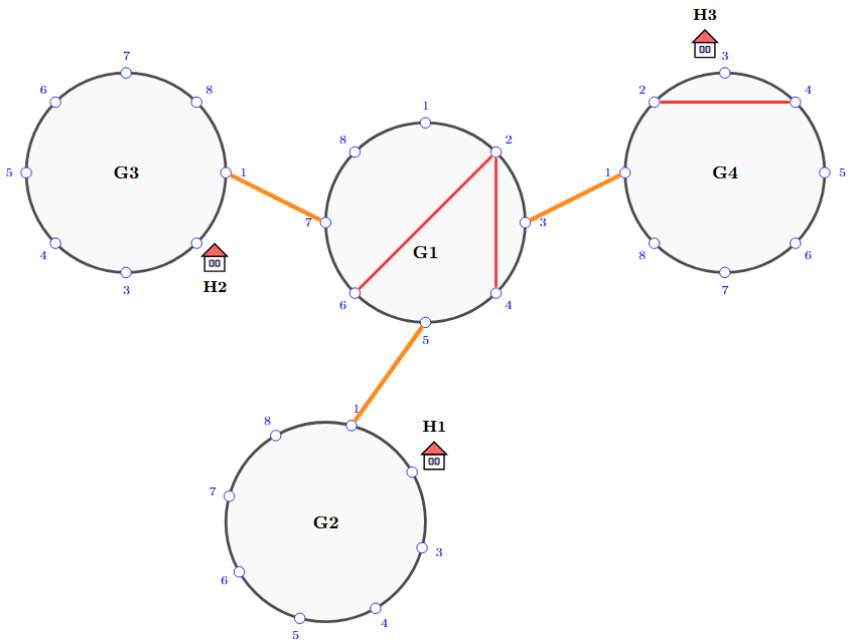
The path between rest house ~1~ and ~2~ passes through ~1~ red path ~(2, 6)~ of garden 1.

The path between rest house ~1~ and ~3~ passes through ~2~ red paths ~(2, 6)~ of garden 1 and ~(2, 4)~ of garden 4.

The path between rest house ~2~ and ~3~ passes through ~3~ red paths ~(2, 6), (2, 4)~ of garden 1 and ~(2, 4)~ of garden 4.

The total score is: ~1 + 2 + 3 = 6~