Bedao Regular Contest 20
Điểm: 100
Với mỗi số nguyên ~n~ cho trước, bạn hãy đếm số cặp số ~(a, b)~ (~a, b~ chẵn; ~a, b > 0~) sao cho ~a \cdot a \cdot b \cdot b = n~.
Lưu ý: Cặp ~(a, b)~ có kể thứ tự. Ví dụ, ~(1, 2)~ và ~(2, 1)~ là hai cặp số khác nhau.
Input
Dòng đầu tiên gồm số nguyên dương ~t~ ~(1 \le t \le 20)~ — số bộ test.
~t~ dòng tiếp theo, mỗi dòng gồm một số nguyên dương ~n~ ~(0 < n \le 10^{18})~.
Output
- In ra ~t~ dòng, mỗi dòng gồm một số nguyên là số cặp thoả mãn.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~10\%~ | ~n \le 10^{6}~ |
| ~2~ | ~30\%~ | ~n \le 10^{12}~ |
| ~3~ | ~60\%~ | ~n \le 10^{18}~ |
Sample Input 1
2
144
72
Sample Output 1
2
0
Notes
Trong testcase thứ 1, các cặp số thoả mãn là: ~(2, 6)~, ~(6, 2)~.
Trong testcase thứ 2, không tồn tại cặp số thoả mãn.
Điểm: 100
Lại một mùa thi Olympic 30/4 nữa sắp tới. Bạn B. giấu tên, người đã từng tham gia kì thi này ở năm lớp 10, đã có phần thể hiện không quá thành công với kết quả là đồng rách. Một trong những lí do chính là do bạn quá tập trung quá một bài và không đủ thời gian cho những bài khác. Hiện tại bạn ấy đang luyện tập cho kì thi. Dựa vào trình độ thượng thừa, bạn ấy biết với thực lực của bản thân có thể giải được một bài mất bao nhiêu thời gian.
Đề thi gồm ~3~ bài và thời gian là ~180~ phút, điểm số từng bài lần lượt là ~6~, ~7~, ~7~. Mỗi bài gồm tối thiểu ~1~ subtask và tối đa ~6~ subtask (subtask là các ý nhỏ của bài chiếm một lượng điểm của bài, đôi lúc cũng là ý tưởng để đẩy lên các sub cao hơn). Mỗi subtask sẽ chiếm trọng số điểm nhất định của bài và tốn một lượng thời gian nhất định để làm. Ngoài ra, để làm được một subtask bất kỳ, bạn có thể phải làm trước một số subtask khác của bài.
Dù trình cao nhưng rất tiếc là với ~180~ phút ít ỏi, bạn B. cũng không thể làm full đề được. Vì thế B. muốn nhờ bạn tìm một chiến lược hợp lí để đạt điểm số cao nhất với tổng thời gian không quá ~180~ phút.
Input
Dữ liệu đầu vào gồm ~3~ bài, mỗi bài cách nhau bằng một khoảng trắng.
Dòng đầu của mỗi bài gồm một số nguyên dương ~K~ là số lượng subtask của bài đó (~1 \leq K \leq 6~). Với mỗi subtask ~i~ trong ~K~:
Dòng đầu gồm ~3~ số nguyên ~t_i~, ~d_i~, ~e_i~ (~1 \leq t_i \leq 180~, ~1 \leq d_i \leq 100~, ~0 \leq e_i \lt i~) lần lượt là thời gian làm, phần trăm điểm và số subtask cần làm trước của subtask đó. Đầu vào đảm bảo ~\sum_{i = 1}^{K} d_i = 100~.
Dòng thứ hai gồm ~e_i~ số nguyên dương ~s_1, s_2, \cdots, s_{e_i}~ (~1 \leq s_j \lt i~) cho biết các subtask cần giải trước để làm được subtask này. Lưu ý rằng bạn không cần giải các subtask này theo thứ tự, bạn chỉ cần giải hết chúng trước là được.
Output
Ghi ra một số thực duy nhất là điểm số tối đa bạn B. có thể đạt được, làm tròn đến 2 chữ số sau phần thập phân.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~30~ | ~e_i = 0~ |
| 2 | ~70~ | Không có ràng buộc gì thêm |
Sample Input 1
3
10 30 0
20 20 0
40 50 1
2
2
10 50 0
100 50 1
1
3
10 30 0
10 20 0
170 50 1
2
Sample Output 1
13.50
Notes
Cách làm tối ưu là:
Làm các subtask ~1~, ~2~ của bài ~1~ trong ~30~ phút được ~3~ điểm.
Làm các subtask ~1~, ~2~ của bài ~2~ trong ~110~ phút được ~7~ điểm.
Làm các subtask ~1~, ~2~ của bài ~3~ trong ~20~ phút được ~3.5~ điểm.
Số điểm bạn B. đạt được là ~13.50~ với thời gian làm là ~160~ phút.
Lưu ý: Bạn cần in ra chính xác 2 chữ số sau phần thập phân. Ví dụ, nếu kết quả là ~8~, output duy nhất được chấp nhận là "~8.00~".
Điểm: 100
HuyAT là học sinh trường P giấu tên mới thi kỳ thi V giấu tên. Vì cay cú khi choke, anh ấy đã chơi một trò để tịnh tâm lại. Trò chơi được mô tả như sau.
Ban đầu có ~N~ chồng đá, chồng thứ ~i~ có ~A_i~ viên đá. Ở mỗi lượt đi, HuyAT có thể mua ~1~ viên đá giá ~C_1~ hoặc ~2~ viên đá với giá ~C_2~. Sau khi mua đá xong thì HuyAT sẽ đặt những viên đá mình mua vòng các chồng đá. Ở mỗi lượt, mỗi chồng đá chỉ được đặt đá vào tối đa một lần. Trò chơi kết thúc khi mọi chồng đá có cùng độ cao.
Vì tiếc tiền, HuyAT muốn dùng ít tiền nhất để hoàn thành trò chơi. Hãy giúp HuyAT nhé.
Input
Dòng đầu tiên gồm ba số nguyên ~N, C_1, C_2~ ~(1 \le N \le 10^5, 1 \le C_1, C_2 \le 10^5)~.
Dòng thứ hai gồm ~N~ số nguyên là mảng ~A~ ~(1 \le A_i \le 10^6)~.
Output
- In ra một số nguyên là số tiền tối thiểu để hoàn thành trò chơi.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~20\%~ | ~C_1 \times 2 \le C_2~ |
| ~2~ | ~20\%~ | ~C_1\le C_2~ |
| ~3~ | ~30\%~ | ~N\le 1000, A_i\le 1000~ |
| ~4~ | ~30\%~ | Không có ràng buộc gì thêm |
Sample Input 1
2 15 3
1 4
Sample Output 1
45
Sample Input 2
5 10 4
2 11 11 11 12
Sample Output 2
54
Notes
Giải thích test ví dụ:
- Ở test đầu tiên, ta mua ~3~ viên đá ở ~3~ lượt và đều đặt chúng vào chồng thứ nhất.
Điểm: 100
Bạn có một mảng gồm ~n~ số nguyên ~a_1, a_2, \dots, a_n~. Vào ngày thứ ~i~ trong ~d~ ngày, bạn phải thực hiện chính xác ~1~ trong ~2~ thao tác sau đây:
Thêm ~1~ vào ~b_i~ phần tử đầu tiên của mảng ~a~ ~(a_j = a_j + 1~ với ~1 \le j \le b_i)~
Thêm số lượng số có giá trị bằng chính vị trí của nó ~(a_j = j)~ vào điểm của bạn và khởi tạo lại mảng ~a~ với giá trị ~0~ ~([a_1, a_2, \dots, a_n] = [0, 0, \dots, 0])~.
Điểm ban đầu của bạn là ~0~. Lưu ý rằng bạn phải thực hiện chính xác một thao tác trong hai thao tác đã nói ở trên, cũng như không thể bỏ qua ngày nào hay thực hiện cả hai thao tác cùng một ngày.
Điểm cao nhất mà bạn có thể đạt được sau ~d~ ngày là bao nhiêu?
Do ~d~ rất lớn, mảng ~b~ sẽ được nén theo dạng sau:
Bạn được cho một mảng ~v~ gồm ~k~ phần tử: ~v_1, v_2, \dots, v_k~;
Mảng ~b~ sẽ là: ~[v_1, v_2, \dots, v_k, v_1, v_2, \dots, v_k, \dots]~.
Input
Dòng đầu tiên gồm ba số nguyên ~n, k, d~ ~(1 \le n, k \le 10^5, k \le d \le 10^9)~.
Dòng thứ hai gồm ~n~ số nguyên ~a_1, a_2, \dots, a_n~ ~(0 \le a_i \le n)~.
Dòng thứ ba gồm ~k~ số nguyên ~v_1, v_2, \dots, v_k~ ~(1 \le v_i \le n)~.
Output
- In ra một số duy nhất là điểm tối đa bạn có thể đạt được sau ~d~ ngày.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10\%~ | ~d \le 10, n \le 10^3~ |
| 2 | ~10\%~ | ~n \le 5 \cdot 10^3~ và ~a_1 = a_2 = \dots = a_n~ |
| 3 | ~30\%~ | ~n \le 5 \cdot 10^3~ |
| 4 | ~50\%~ | Không có ràng buộc gì thêm. |
Sample Input 1
3 4 4
1 2 3
1 3 2 3
Sample Output 1
4
Sample Input 2
3 1 1
0 0 1
1
Sample Output 2
0
Notes
Giải thích test đề ~1~:
Ở ngày đầu tiên, bạn chọn thao tác ~2~. Vì cả ~3~ vị trí đều thỏa mãn nên điểm hiện tại của bạn là ~3~. Dãy được khởi tạo lại về ~[0, 0, 0]~.
Ở hai ngày tiếp theo, bạn chọn thao tác ~1~. Dãy trở thành ~[2, 2, 1]~.
Ở ngày cuối cùng, bạn chọn thao tác ~2~. Vị trí ~2~ là vị trí duy nhất thỏa mãn và do đó điểm số được tăng thêm ~1~.
Giải thích test đề ~2~:
- Vì chỉ có ~1~ ngày, bạn chọn thao tác ~2~. Nhưng vì không có vị trí nào thỏa mãn nên đáp án là ~0~.
Điểm: 100
Một xâu được gọi là xâu đối xứng nếu như viết xâu đó từ trái sang phải giống cách viết xâu ấy từ phải sang trái. Ví dụ về xâu đối xứng là "ioi", "madam", ~\dots~ Ví dụ về xâu không phải xâu đối xứng là "vnoi", "abab", ~\dots~
Gọi ~F(T)~ là độ dài của xâu con liên tiếp dài nhất của ~T~ mà không phải là xâu đối xứng. Ví dụ: ~F(~"ioi"~) = 2~, ~F(~"vnoi"~) = 4~, ~F(~"zzz"~) = 0~.
Cho một xâu ~S~ có độ dài ~N~ gồm các chữ cái viết thường. Một chữ cái ~c~ được gọi là thực hiện bước nhảy là khi ta thay thế ~c~ bằng chữ cái sau chữ cái ~c~ trong bảng alphabet, riêng chữ cái sau z là chữ a. Thao tác ~C(i, k)~ sẽ làm cho kí tự ~S_i~ thực hiện bước nhảy ~k~ lần.
Ta có ~Q~ truy vấn, mỗi truy vấn thuộc một trong ~2~ loại sau đây:
~1~ ~l~ ~r~ ~k~ ~(1 \le l \le r \le N, 0 \le k \le 10^9)~: Thực hiện thao tác ~C(i, k)~ với tất cả ~i~ từ ~l~ tới ~r~.
~2~ ~l~ ~r~ ~(1 \le l \le r \le N)~: In ra ~F(T)~ với ~T~ là xâu con liên tiếp gồm các ký tự từ ~l~ tới ~r~ của ~S~.
Input
Dòng đầu tiên gồm ~2~ số nguyên ~N, Q~ ~(1 \le N, Q \le 10^5)~ — độ dài của xâu ~S~ và số lượng truy vấn.
Dòng thứ hai chứa xâu ~S~.
~Q~ dòng cuối cùng, mỗi dòng có dạng thuộc một trong ~2~ loại đã nói ở trên.
Output
- Với mỗi truy vấn loại ~2~, in ra đáp án của truy vấn trên một dòng.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~5\%~ | ~1 \le N, Q \le 10^3~ |
| 2 | ~10\%~ | ~k = 0~ với mọi truy vấn loại ~1~ |
| 3 | ~20\%~ | ~l = r~ với mọi truy vấn loại ~1~ |
| 4 | ~15\%~ | Các truy vấn loại ~1~ xảy ra trước các truy vấn loại ~2~ |
| 5 | ~50\%~ | Không có ràng buộc gì thêm |
Sample Input 1
3 3
uwu
2 1 3
1 2 3 4
2 2 3
Sample Output 1
2
2
Sample Input 2
10 3
toiyeuvnoi
2 5 10
1 1 9 21
2 8 10
Sample Output 2
6
2
Notes
Giải thích bộ test thứ nhất:
Ban đầu, ~S~ = "uwu".
Truy vấn ~1~, ~F(~"uwu"~) = 2~, xâu con dài nhất thõa mãn có thể là "uw" hoặc "wu".
Truy vấn ~2~, ~S_2 =~ w lần lượt nhảy tới x, y, z, và rồi tới a, còn ~S_3 =~ u sau ~4~ lần nhảy sẽ nhảy tới y. Do đó lúc này ~S =~ "uay".
Truy vấn ~3~, ~F(~"ay"~) = 2~, xâu con thỏa mãn dài nhất là chính nó.
Điểm: 100
Dd đang chơi Terraria và vừa mở khóa được vũ khí mới: North Pole.
Mỗi lần sử dụng, vũ khí này bắn một quả cầu tuyết tại vị trí ~(s_i, 0)~ với vector vận tốc ~\vec{v_i} = ({v_x}_i, {v_y}_i)~. Ta giả sử gia tốc trọng trường ~G = 9.8~ và không có lực cản của không khí.
Trên đường bay của quả cầu tuyết sẽ xuất hiện các bông tuyết rơi thẳng đứng và khi rơi xuống sẽ gây sát thương. Quả cầu tuyết biến mất khi chạm đất. Trong bài toán này, có vô số bông tuyết được tạo ra, nghĩa là nếu người chơi đứng dưới đường bay của một quả cầu tuyết thì chắc chắn sẽ bị sát thương.

Demo của vũ khí North Pole.
Yêu cầu: Tính tổng diện tích trên bản đồ mà người chơi đứng ở đó sẽ bị sát thương.
Input
Dòng đầu tiên gồm số nguyên ~n \:(1 \le n \le 1000)~ — số lần Dd sử dụng vũ khí.
~n~ dòng tiếp theo, mỗi dòng gồm 3 số nguyên ~s_i, {v_x}_i, {v_y}_i \:(0 \le s_i \le 10^9, 1 \le {v_x}_i, {v_y}_i \le 1000)~ — tọa độ và vận tốc của cầu tuyết thứ ~i~.
Output
- In ra một dòng duy nhất chứa 1 số thập phân — đáp án của bài toán. Đáp án được chấp nhận nếu sai số không quá ~10^{-6}~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~15\%~ | Không có quỹ đạo của 2 cầu tuyết nào giao nhau hoặc nằm trong nhau. |
| 2 | ~25\%~ | ~n \le 100~ |
| 3 | ~60\%~ | Không có ràng buộc gì thêm. |
Sample Input 1
1
0 1 1
Sample Output 1
0.0069415521
Sample Input 2
2
0 3 5
2 5 2
Sample Output 2
2.7463907059
Notes
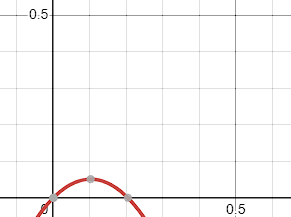
Quỹ đạo cầu tuyết trong ví dụ 1.
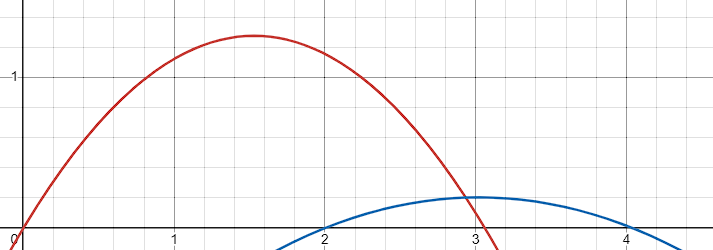
Quỹ đạo các cầu tuyết trong ví dụ 2.