Người Ai Cập cổ đại đã bắt đầu xây dựng các kim tự tháp một thời gian ngắn sau năm ~2700~ trước công nguyên, thời kì hoàng kim của các kim tự tháp dành cho hoàng tộc kéo dài khoảng ~1000~ năm, đến năm ~1700~ trước công nguyên. Trong đó, lớn nhất cũng như nổi tiếng nhất là kim tự tháp tại thành phố ~Giza~, trong đó bao gồm kim tự tháp ~Giza~ của Pharaoh Khufu.

Lấy cảm hứng từ các kim tự tháp của người Ai Cập cổ, Soen đã tạo ra một cái của riêng mình bằng cách sử dụng những con số. Kim tự tháp của Soen được miêu tả gồm cặp số ~(m, n)~. Bắt đầu từ số ~1~, tăng dần đến ~m~ và sau đó lại giảm dần về ~1~, quá trình này sẽ được lặp lại ~n~ lần. Cuối cùng, Soen thắc mắc tổng các số trên kim tự tháp của mình là bao nhiêu, các bạn hãy giúp Soen nhé.

Input:

• Dòng đầu gồm số nguyên ~Q~ là số lượng truy vấn ~(1 \leq Q \leq 10^5)~
• ~Q~ dòng sau, mỗi dòng gồm ~2~ số nguyên ~n, m~ thể hiện dữ liệu kim tự tháp của truy vấn tương ứng ~(1 \leq n, m \leq 10^9)~

Output:

• Gồm ~Q~ dòng, mỗi dòng gồm một số nguyên là tổng các số trên kim tự tháp ~(m, n)~ đó. Vì kết quả có thể rất lớn các bạn hãy in kết quả là phần dư của phép chia khi chia kết quả cho ~10^9 + 7~

Sample Input

1
4 3

Sample Output

33

Subtask

• ~20\%~ số test có ~Q = 1; 1 \leq n, m \leq 10^3~
• ~20\%~ số test tiếp theo có ~Q \le 10^5; 1 \leq n, m \leq 10^3~
• ~60\%~ số test còn lại có ~Q \le 10^5; 1 \leq n, m \leq 10^9~

Nhận thấy sắp tới ngày quốc tế thiếu nhi (International Children's Day), trường tiểu học Bedao tổ chức một số hoạt động chào mừng, trường sẽ tổ chức một buổi phát kẹo. Trường dự định phát kẹo cho ~N~ em học sinh nhưng với bản tính tương thân tương ái "có bao nhiêu chia bấy nhiêu" các em thường sẽ lấy số kẹo của mình chia đều cho các em có số thứ tự lớn hơn mình, sau cùng sẽ giữ lại phần không thể chia. Hay với em học sinh có số thứ tự ~i~ thì em sẽ chia kẹo mình cho em học sinh số thứ tự ~j~ sao cho ~(i < j)~ và số kẹo học sinh ~i~ chia cho từng em học sinh ~j~ sẽ như nhau. Hỏi sau khi phát kẹo và các em học sinh chia kẹo cho nhau xong thì số kẹo của từng em học sinh sẽ là bao nhiêu ?

Input

• Dòng thứ nhất chứa ~1~ số nguyên ~N~ ~(1 \le N \le 10^6)~.
• Dòng thứ hai chứa ~N~ số nguyên dương ~A_1, A_2 , \dots , A_N~ ~(1 \le A_i \le 10^9)~, mỗi số được cách nhau bởi ~1~ dấu cách.

Output

• Ghi ra ~N~ số nguyên dương là số kẹo sau cùng của ~N~ học sinh.

Sample Input

3 
3 2 1

Sample Output

1 0 5

Subtask

• ~50\%~ số test có ~N \le 3000~
• ~50\%~ số test tiếp theo có ~N \le 10^6~

Note

• Em học sinh ~1~ chia cho em học sinh ~2~ và ~3~ mỗi em ~1~ cái kẹo. Số kẹo giờ còn là ~[1 , 3 , 2]~.
• Em học sinh ~2~ chia cho em học sinh ~3~ ~3~ cái kẹo . Số kẹo giờ còn là ~[1 , 0 , 5]~.

Ở một ngôi trường nọ, có một quy tắc mà học sinh nào cũng biết đó là "ôn thi một đằng kiểm tra một nẻo".

Vào một ngày mưa rào, tâm tình gắt gỏng nên cô của Neko vừa cho ôn dạng bài tìm tích của ~2~ số thì đã cho làm bài kiểm tra và bắt Neko phải tìm ra được tổng của tích tất cả các bộ ~3~ số ~a_i, a_j, a_k~ trong ~n~ số ~(1 \le i < j < k \le n)~. Vì quá sốc văn hóa nên Neko đành phải nhờ bạn lập trình giải giúp bài toán này. Do kết quả có thể là số rất lớn nên Neko yêu cầu bạn phải lấy phần dư khi chia kết quả cho ~10^9 + 7~.

Input

• Dòng đầu chứa số nguyên dương ~n~ ~(1 \le n \le 10^5)~.
• Dòng thứ hai chứa ~n~ số nguyên dương ~a_1, a_2, a_3, ..., a_n~ ~(1 \leq a_i \le 10^6)~.

Output

• Ghi ra tổng của tích tất cả các bộ ~3~ số trong ~n~ số.

Sample Input

5
3 2 5 4 6

Sample Output

580

Subtask

• ~10\%~ số test có ~n \le 500~ và ~a_i \le 10^4~
• ~10\%~ số test tiếp theo có ~n \le 5000~
• ~80\%~ số test còn lại không có điều kiện gì thêm

Đô thị học viện là một nơi có công nghệ phát triển bậc nhất hành tinh B. Nơi đây nổi tiếng với việc đào tạo ra những siêu năng lực gia có sức mạnh to lớn. Misaka Mikoto là một trong những siêu năng lực gia mạnh nhất của thành phố. Gekota là một linh thú linh vật mà cô rất thích. Cô thích mọi thứ về Gekota, hôm nay lại có một cuộc thi về trí nhớ mà phần thưởng là một chiếc điện thoại có hình dáng của Gekota.

BTC cuộc thi sẽ đưa ra một hình hộp chữ nhật được ghép từ các khối vuông có kích thước ~1 \times 1 \times 1~ và bên trong mỗi khối vuông sẽ chứa một con số có ~X~ ~(|X| \leq 10^9)~. Vị trí của các khối vuông được biểu diễn bởi ~3~ số nguyên dương ~(x,y,z)~ ứng với tọa độ thuộc hệ trục tọa độ ~Oxyz~.

Người chơi sẽ phải dùng siêu năng lực của mình để nhìn thấu hết các số trong từng ô vuông và tọa độ tương ứng của nó. Theo như thể thức chương trình hàng năm, BTC sẽ đưa ra các câu hỏi có dạng ~(x_1, y_1, z_1; x_2, y_2, z_2)~ yêu cầu người chơi tính tổng các số có tọa độ ~(x, y, z)~ thỏa mãn ~(x_1 \leq x \leq x_2, y_1 \leq y \leq y_2, z_1 \leq z \leq z_2)~ và người trả lời nhanh nhất sẽ nhận được ~1~ điểm. Người nào trả lời đúng càng nhiều thì phần thưởng sẽ càng lớn.

Nhưng để thử thách người chơi năm nay, BTC đã chuẩn bị một hình hộp chữ nhật có kích thước ~m \times n \times p~ gồm các ô vuông ~1 \times 1 \times 1~ có thể thay đổi giá trị theo thời gian. Tức là trong thời gian chuẩn bị của thí sinh sẽ có ~T~ thời điểm, mỗi thời điểm các ô vuông sẽ có giá trị khác nhau. Ô vuông có tọa độ ~(x, y, z)~ vào thời điểm ~t~ sẽ có giá trị là ~a_{x,y,z,t}~ và mỗi câu hỏi lần này lại có dạng ~(x_1, y_1, z_1, t_1; x_2,y_2,z_2,t_2)~ tức là yêu cầu tính tổng các giá trị ~a_{x,y,z,t}~ thỏa mãn ~(x_1 \leq x \leq x_2, y_1 \leq y \leq y_2, z_1 \leq z \leq z_2, t_1 \leq t \leq t_2)~. Tuy thể thức câu hỏi thay đổi nhưng thể thức tính điểm vẫn giữ nguyên: có tổng cộng ~T~ câu hỏi, mỗi câu trả lời đúng và nhanh nhất sẽ nhận được ~1~ điểm và khi đạt được một mức điểm nhất định thì sẽ nhận được phần thưởng ở mốc đó. Đương nhiên để nhận được phần thưởng đặc biệt thì phải đạt được ~T~ điểm, tức là cô phải trả lời đúng và nhanh nhất hết toàn bộ ~T~ câu hỏi. Bạn hãy giúp Misaka Mikoto nhé.

Input

• Dòng đầu tiên chứa ~4~ số nguyên dương ~n~, ~m~, ~p~, ~q~ ~(m, n, p, q \leq 40)~.
• Dòng thứ hai gồm ~n \times m \times p \times q~ các giá trị ~a_{1,1,1,1} , a_{1,1,1,2} ,\dots, a_{1,1,1,q}, a_{1,1,2,1}, \dots, a_{1,1,2,q}, \dots, a_{1,1,p,q}, \dots, a_{1,n,p,q}, \dots,a_{m,n,p,q}~ ~(a_{x,y,z,t} \leq 10^9)~.
• Dòng tiếp theo là một số nguyên dương ~T~ cho biết số câu hỏi mà chương trình đặt ra ~(1 \leq T \leq 10000)~.
• ~T~ dòng tiếp theo là các câu hỏi có dạng ~(x_1, y_1, z_1, t_1; x_2,y_2,z_2,t_2)~ với ~(x_1 \leq x_2 \leq n, y_1 \leq y_2 \leq m, z_1 \leq z_2 \leq p, t_1 \leq t_2 \leq q)~.

Output

• Gồm ~T~ dòng, mỗi dòng là tổng của các giá trị ~a_{x,y,z,t}~ thỏa mãn ~(x_1 \leq x_i \leq x_2, y_1 \leq y_i \leq y_2, z_1 \leq z_i \leq z_2, t_1 \leq t_i \leq t_2)~

Sample Input

2 2 2 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
3
1 1 1 1 2 2 2 2
2 2 1 1 2 2 2 2
1 1 2 2 2 2 2 2

Sample Output

136
58
40

Subtask

• ~30\%~ số test là ~n,m,p,q \leq 10~
• Số test còn lại không giới hạn gì thêm.

Vào lễ Halloween hàng năm, các đứa trẻ thường ghé thăm những ngôi nhà để được phát kẹo. Copium là một người rất hào phóng nên đã chuẩn bị tươm tất các loại kẹo ở nhà để phát cho những đứa trẻ gõ cửa nhà mình. Ban đầu có sẵn ~n~ viên kẹo được chia vào ~m~ túi quà, nhưng để đảm bảo đứa trẻ nào cũng có phần nên Copium muốn mọi túi quà đều có đúng ~k~ viên kẹo. Vì vậy, mỗi lần anh ấy sẽ chọn ra ~1~ túi quà rồi thêm hoặc bớt tùy ý ~1~ viên kẹo từ túi quà đó (hiển nhiên là số kẹo không được âm).

Đếm số cách chia ~n~ viên kẹo vào các túi quà ban đầu sao cho:

• Số túi quà ~m~ là tối đa ~(~vài túi quà có thể không chứa kẹo nên số kẹo mỗi túi phải lớn hơn hoặc bằng ~0~~)~.
• Số lần thêm bớt tối thiểu để mọi túi quà đều có ~k~ viên kẹo là số lần thêm bớt tối thiểu để các túi quà có cùng lượng kẹo.
• Với mọi cặp số ~i, j~ ~( 1 \leq i, j \leq m )~, nếu túi quà thứ ~i~ có ít hơn ~k~ viên kẹo và túi quà thứ ~j~ có từ ~k~ viên kẹo trở lên thì ~i < j~.

Input

• Một dòng gồm ~2~ số nguyên lần lượt là ~n~ và ~k~, là số viên kẹo và số viên kẹo Copium muốn có trong mỗi túi quà ~( 1 \leq n, k \leq 10^{14} )~.

Output

• Số cách chia thỏa mãn yêu cầu đề bài, do đáp án có thể rất lớn nên in ra phần chia dư cho ~10^9+7~.

Sample Input

5 2

Sample Output

4

Note

Có ~4~ cách chia kẹo thỏa mãn, với số túi quà tối đa là ~m = 4~:

• ~[0, 1, 2, 2]~
• ~[1, 0, 2, 2]~
• ~[0, 0, 3, 2]~
• ~[0, 0, 2, 3]~

Subtask

• ~40\%~ số test có ~1 \leq n, k \leq 2 \times 10^6~.
• ~60\%~ số test còn lại không có điều kiện gì thêm.

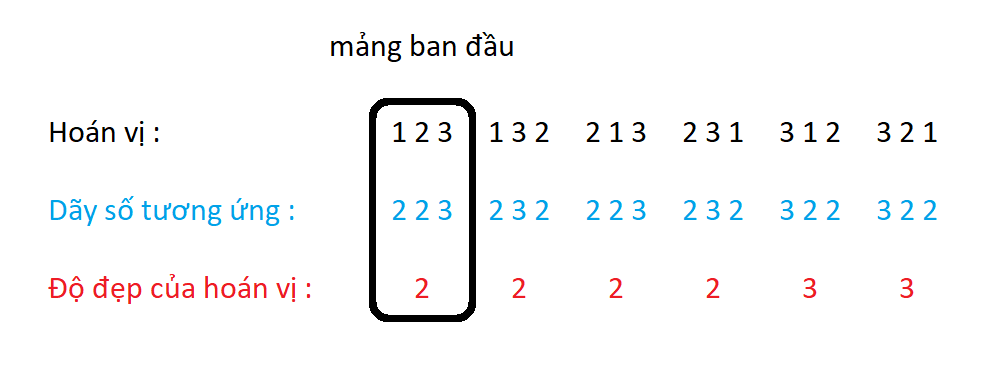
Trung vị của một dãy số có ~n~ phần tử là giá trị phần tử thứ ⌊~\frac{n+1}{2}~⌋ của dãy số đó sau khi được xếp lại theo thứ tự không giảm

Ví dụ : dãy số ~4, 3, 6, 5~ khi xếp lại là ~3, 4, 5, 6~ nên sẽ có trung vị là ~4~. Tương tự, dãy số ~3, 2, 3~ có trung vị là ~3~.

Cho mảng ~a~ gồm ~N~ số nguyên dương, ban đầu các phần tử được xếp theo thứ tự không giảm nhưng mảng ~a~ có thể được hoán vị một cách tùy ý. Ta kí hiệu tiền tố có độ dài ~M~ của mảng ~a~ sau khi hoán vị là ~a_1, a_2, \dots, a_M~ ~(M \leq N)~ và ~MED()~ là hàm tính trung vị của ~1~ dãy số. Với mỗi hoán vị của mảng ~a~, độ đẹp của hoán vị được định nghĩa là ~max(MED(a_1, a_2, \dots, a_M))~ với mọi ~M~ thuộc ~[1, N]~ hay nói cách khác là trung vị lớn nhất có thể lấy được từ các tiền tố của hoán vị đó.

Hãy tính tổng độ đẹp của tất cả ~N!~ hoán vị từ mảng ~a~ ban đầu.

Input

• Vì số phần tử trong mảng ~a~ khá lớn nên input của bài được cho dưới dạng nén.
• Dòng đầu là số nguyên ~k~, số giá trị phân biệt của các phần tử trong mảng ~a~ ~(1 \leq k \leq 2 \times 10^5)~.
• ~k~ dòng tiếp theo, ở dòng thứ ~i+1~ có ~1~ cặp số là ~val_i~ ~(1 \leq val_i \leq 10^9)~ và ~cnt_i~ ~(1 \leq N = \sum_{i = 1}^{k} cnt_i \leq 2 \times 10^6)~ trong đó ~val_i~ là giá trị bé thứ ~i~ trong mảng ~a~ và ~cnt_i~ là số lần xuất hiện của giá trị ~val_i~ ~(~dữ liệu đảm bảo nếu ~i < j~ thì ~val_i < val_j~~)~.

Output :

• In ra tổng độ đẹp của các hoán vị chia lấy dư cho ~10^9+7~.

Sample Input

2
2 2
3 1

Sample Output

14

Subtask:

• ~10\%~ số test có ~cnt_k \geq 10^6~.
• ~30\%~ số test có ~k = 2~ và ~cnt_1 = cnt_2~.
• ~60\%~ số test còn lại không còn điều kiện gì thêm.

Note

• Giải thích sample test :