Bedao Regular Contest 06 - PMED
Xem dạng PDFTrung vị của một dãy số có ~n~ phần tử là giá trị phần tử thứ ⌊~\frac{n+1}{2}~⌋ của dãy số đó sau khi được xếp lại theo thứ tự không giảm
Ví dụ : dãy số ~4, 3, 6, 5~ khi xếp lại là ~3, 4, 5, 6~ nên sẽ có trung vị là ~4~. Tương tự, dãy số ~3, 2, 3~ có trung vị là ~3~.
Cho mảng ~a~ gồm ~N~ số nguyên dương, ban đầu các phần tử được xếp theo thứ tự không giảm nhưng mảng ~a~ có thể được hoán vị một cách tùy ý. Ta kí hiệu tiền tố có độ dài ~M~ của mảng ~a~ sau khi hoán vị là ~a_1, a_2, \dots, a_M~ ~(M \leq N)~ và ~MED()~ là hàm tính trung vị của ~1~ dãy số. Với mỗi hoán vị của mảng ~a~, độ đẹp của hoán vị được định nghĩa là ~max(MED(a_1, a_2, \dots, a_M))~ với mọi ~M~ thuộc ~[1, N]~ hay nói cách khác là trung vị lớn nhất có thể lấy được từ các tiền tố của hoán vị đó.
Hãy tính tổng độ đẹp của tất cả ~N!~ hoán vị từ mảng ~a~ ban đầu.
Input
- Vì số phần tử trong mảng ~a~ khá lớn nên input của bài được cho dưới dạng nén.
- Dòng đầu là số nguyên ~k~, số giá trị phân biệt của các phần tử trong mảng ~a~ ~(1 \leq k \leq 2 \times 10^5)~.
- ~k~ dòng tiếp theo, ở dòng thứ ~i+1~ có ~1~ cặp số là ~val_i~ ~(1 \leq val_i \leq 10^9)~ và ~cnt_i~ ~(1 \leq N = \sum_{i = 1}^{k} cnt_i \leq 2 \times 10^6)~ trong đó ~val_i~ là giá trị bé thứ ~i~ trong mảng ~a~ và ~cnt_i~ là số lần xuất hiện của giá trị ~val_i~ ~(~dữ liệu đảm bảo nếu ~i < j~ thì ~val_i < val_j~~)~.
Output :
- In ra tổng độ đẹp của các hoán vị chia lấy dư cho ~10^9+7~.
Sample Input
2
2 2
3 1
Sample Output
14
Subtask:
- ~10\%~ số test có ~cnt_k \geq 10^6~.
- ~30\%~ số test có ~k = 2~ và ~cnt_1 = cnt_2~.
- ~60\%~ số test còn lại không còn điều kiện gì thêm.
Note
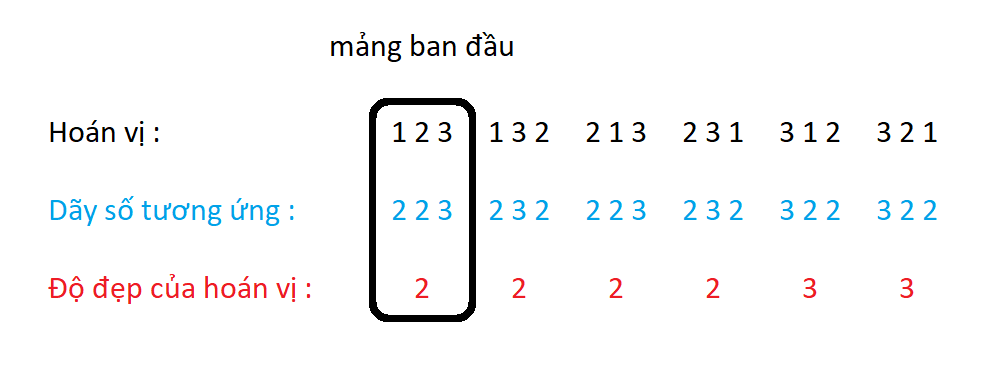
- Giải thích sample test :
Bình luận