Trong ngày ~20/11~, lớp Bedao có ~n~ người muốn chơi một trò chơi dân gian mang đậm chất tình thương mến thương. Sau một hồi tranh luận, cả lớp quyết định sẽ chơi trò chơi nối chữ. Luật chơi như sau:

Có ~n~ lượt:

• Lượt đầu người chơi ~1~ sẽ nói ~1~ từ.

• Lượt hai người chơi ~2~ sẽ nói ~1~ từ.

• ~\dots~

Trò chơi sẽ tiếp diễn cho đến khi tìm ra được người thua hoặc đã hết lượt mà không có ai vi phạm luật.

Một người chơi sẽ bị xử thua nếu họ nói lại từ mà một trong những người trước đã nói hoặc chữ cái đầu tiên của từ vừa nói không giống với chữ cái cuối của từ nói trước đó.

Thế nhưng vì số lượng thành viên trong lớp Bedao quá lớn nên họ yêu cầu bạn tạo ra chương trình để kiếm tra xem có ai vi phạm luật chơi hay không.

Input

• Dòng đầu tiên chứa số nguyên dương ~n~. ~(1 \le n \le 5 \times 10^{5})~

• Dòng thứ 2 chứa ~n~ xâu ký tự ~s_1, s_2, ..., s_n,~ xâu ~s_i~ là từ mà người thứ ~i~ nói. ~ (1 \le |s_i| \le 20)~

Output

• In ra ~YES~ nếu dãy từ thỏa mãn yêu cầu đề bài. Ngược lại in ra ~NO~ và số thứ tự của người chơi vi phạm.

• Trong trường hợp nhiều người vi phạm, hãy in ra số thứ tự của người vi phạm đầu tiên.

Sample Input

5
adega ayuta a ate electronic

Sample Output

YES

Sample Input

6
ti huhu uranium meme exe origami

Sample Output

NO
2

iostream nổi tiếng là một người hiền lành, vì thế iostream luôn giao những công việc đơn giản cho dao-puppy. Hôm nay cũng vậy, iostream đưa cho dao-puppy môt chương trình mã hóa xâu và một xâu ~S~ có độ dài không vượt quá ~10^5~ kí tự chỉ gồm các chữ cái Latin thường. Chương trình mã hóa xâu sẽ hoạt động như sau:

Người dùng cần nhập vào chương trình một xâu có ít nhất ~2~ kí tự. Sau đó chương trình sẽ chọn ngẫu nhiên ~2~ số ~i~ và ~j~ khác nhau, đổi chỗ ~2~ kí tự ở ~2~ vị trí này rồi trả cho người dùng xâu sau khi đổi chỗ (hai chỉ số ~i, j~ không vượt quá độ dài của xâu).

Ví dụ xâu nhập vào là ~aba~, chương trình chọn được ~2~ số ~i~ và ~j~ là ~1~ và ~2~ thì chương trình sẽ trả về xâu ~baa~.

Dễ thấy rằng với cùng một xâu có thể cho ra nhiều kết quả mã hóa khác nhau. iostream muốn nhờ dao-puppy giúp mình ghi lại tất cả các xâu khác nhau có thể nhận được khi cho máy mã hóa xâu ~S~.

Bằng cách đưa xâu ~S~ vào chương trình mã hóa nhiều lần, dao-puppy đã ghi ra được rất nhiều xâu khác nhau nhưng không biết đã đủ hay chưa, bạn hãy giúp dao-puppy tính xem có tất cả bao nhiêu xâu khác nhau có thể nhận được bằng việc mã hóa xâu ~S~.

Input

• Một dòng duy nhất chứa xâu ~S~ ~(2 \leq |S| \leq 10^5)~

Output

• In ra số xâu khác nhau có thể nhận được

Sample Input

abca

Sample Output

6

Note

Các xâu khác nhau nhận được là ~abca, baca, cbaa, acba, aacb, abac~.

Hãy đếm số lượng số trong đoạn từ ~a~ đến ~b~ có ~k~ ước nguyên tố khác nhau. Cho ~Q~ truy vấn , mỗi truy vấn gồm ba số nguyên dương ~a, b, k~.

Input

• Dòng đầu tiên chứa số nguyên dương ~Q~ là số lượng truy vấn. ~(1 \leq Q \leq 10^5)~

• ~Q~ dòng tiếp theo, dòng thứ ~i~ chứa ~3~ số nguyên ~a_i, b_i, k_i~ lần lượt mô tả các giá trị như trong yêu cầu bên trên. ~(1 \le a \le b \le 10^6, 1 \le k \le 7)~

Output

• Ứng với truy vấn thứ ~i~, in ra một số nguyên duy nhất là số lượng số trong đoạn ~a_i~ đến ~b_i~ mà có ~k_i~ ước nguyên tố khác nhau. Mỗi truy vấn in ra trên một dòng.

Sample Input

2
3 6 2
7 10 1

Sample Output

1
3

Subtask

• ~40\%~ số test có ~Q, a, b \le 10^3~
• ~60\%~ số test còn lại không có điều kiện gì thêm

Đếm số lượng bộ số ~(a, b, c)~ nguyên dương sao cho ~a \times b \times c \le n~.

Lưu ý: Bộ ~(1, 2, 3)~ vẫn tính là khác so với ~(1, 3, 2)~ hay ~(3, 2, 1)~.

Input

Gồm ~1~ dòng chứa số nguyên dương ~n~. ~(1 \le n \le 10^{9})~

Output

In ra số lượng bộ ba số ~(a, b, c)~ thỏa mãn đề bài.

Sample Input

3

Sample Output

7

Giải thích

Có các bộ ~3~ số là ~(1,1,1), (1,1,3), (1,3,1), (3,1,1), (1,1,2), (1,2,1), (2,1,1)~

Subtask

• ~40\%~ số test có ~1 \le n \le 100~
• ~60\%~ số test còn lại không có điều kiện gì thêm

Như ai cũng biết, chị Hiền là một con người ác độc và có những trò chơi cũng tàn nhẫn không kém tâm hồn chị. Năm nay, cũng như mọi lần, chị Hiền lại tổ chức giải "Đua chó mở rộng", cuộc đua diễn ra trên trục tọa độ ~Oxy~.

Ban đầu, có ~n~ chú chó (bao gồm đủ loại màu sắc chứ không chỉ màu vàng) sẽ tham gia cuộc thi và đứng ở vạch xuất phát (~x = 0~). Về mặt toán học, ta sẽ biểu diễn vị trí đứng của ~n~ chú chó này bằng một mảng ~p~ độ dài ~n~. Chú chó thứ ~i~ sẽ xuất phát ở điểm có tọa độ ~(0, p_i)~.

Đồng thời do chị Hiền không thích việc hai chú chó cắn nhau trước khi chạy đua, dữ liệu đảm bảm rằng mọi vị trí ~p_i~ đều phân biệt. Vạch kết thúc là ~x = k~.

Chó vàng là một trong những dân bet đua chó dạng trùm sỏ, vì thế anh ấy đã bí mật thao túng cuộc thi này. Bây giờ, việc gọi đây là một giải đua chó cũng không hẳn là đúng, vì thật ra mọi chú chó đều sẽ có tốc độ giống nhau!! Sốc hơn nữa, mọi chú chó sẽ không chạy theo đường thẳng, mà sẽ chỉ chạy theo đường chéo về đích. Về mặt toán học, giả sử chú chó thứ ~i~ được phân loại ~t_i~ (với ~t_i~ bằng ~-1~ hoặc ~1~). Nếu:

• ~t_i = -1~, thì chú chó thứ ~i~ sẽ có vận tốc là ~(1, -1)~ trên giây.
• ~t_i = 1~, thì chú chó thứ ~i~ sẽ có vận tốc là ~(1, 1)~ trên giây.

Với một cuộc đua bất công như thế này, va chạm giữa hai "chó thủ" là điều hoàn toàn có thể xảy ra. Vì thế, trước khi bắt đầu, mọi chú chó đã thỏa thuận với nhau cách để xử lí khi có một cặp chó va chạm: hai chú chó va chạm sẽ hoán đổi vận tốc cho nhau. Về mặt toán học, giả sử chó chó ~A~ có loại ~1~ va chạm với chú chó ~B~ có loại ~-1~, thì ngay sau khi va chạm, loại của chú chó ~A~ sẽ trở thành ~-1~, và loại của chú chó ~B~ sẽ trở thành ~1~.

Bạn là người quản lý cuộc đua, để tổng hợp để xem trong cuộc đua có sự bán độ hay không, bạn cần biết hai thông tin sau khi cuộc thi kết thúc:

• Số lượng va chạm đã diễn ra trong cuộc thi ngay trước khi mọi chú chó cán đích. Điều này có nghĩa là va chạm giữa những chú chó trên vạch kết thúc sẽ không được tính.

• Vị trí kết thúc của từng chú chó từ ~1~ đến ~n~.

Input

• Dòng đầu tiên gồm hai số nguyên phân biệt ~n~ và ~k~ (~1 \le n \le 200\,000~, ~1 \le k \le 10^9~) - lần lượt là số lượng chú chó tham gia cuộc thi và tọa độ ~x~ của vạch kết thúc.
• Dòng thứ hai gồm ~n~ số nguyên ~p_1, p_2, \cdots, p_n~ (~-10^9 \le y_i \le 10^9~) - biểu diễn tọa độ ~y~ của ~n~ chú chó trên vạch xuất phất. Dữ liệu đảm bảo rằng mọi ~p_i~ đều phân biệt, hay nói cách khác, ~p_i \ne p_j~ với mọi ~1 \le i < j \le n~.
• Dòng thư ba gồm ~n~ số nguyên ~t_1, t_2, \cdots, t_n~ (~t_i \in \{-1, 1\}~) - biểu diễn loại của ~n~ chú chó.

Output ra

Bạn cần in ra hai dòng:

• Dòng thứ nhất chứa một số nguyên duy nhất - số lượng va chạm đã diễn ra trong cuộc thi ngay trước khi mọi chú chó cán đích.
• Dòng thứ hai chứa ~n~ số nguyên, số nguyên thứ ~i~ biểu diễn tọa độ ~y_i~ là vị trí cán đích của chú chó thứ ~i~.

Sample Input

3 2
1 0 2
1 1 -1

Sample Output

2
2 0 3

Sample Input

2 1
0 2
1 -1

Sample Output

0
1 1

Hình vẽ mô tả test ví dụ 1, đường màu đỏ biểu diễn đường đi của chú chó thứ ~1~, đường màu xanh lam của chú chó thứ ~2~, đường màu xanh lục của chú chó thứ ~3~. Những điểm màu đen biểu diễn va chạm đã xảy ra.

Chovang là một dân chơi kiến thực thụ, tổ kiến của Chovang gồm nhiều đàn kiến thợ và một con kiến chúa, thậm chí những con kiến này như một xã hội thu nhỏ mà mỗi con kiến đều có một phòng cho riêng mình. Chovang đã cẩn thận đánh số từng căn phòng cho lũ kiến của mình lần lượt từ ~1~ đến ~n~ mà trong đó phòng thứ ~1~ chính là của kiến chúa. Ta có thể xem tập hợp các căn phòng này là một đồ thị liên thông vô hướng không chu trình gồm ~n~ nút và ~n - 1~ cạnh. Một cạnh là đường đi nối giữa hai căn phòng khác nhau và cả hai căn phòng đều đi qua lại được với nhau từ hai hướng. Ban đầu, tất cả các đỉnh đều có khả năng đi qua nhau được. Đàn kiến có tập tính là hàng ngày đều đi kiếm thức ăn bên ngoài và đem về tổ phục vụ cho kiến chúa, nhưng chẳng may bọn chim đã đánh hơi được một con kiến rồi biết được tổ kiến của Chovang và rất muốn ăn hết từng con kiến trong tổ. Trận chiến nào cũng cần có sự hi sinh nên Chovang chấp nhận sẽ bỏ mặc một vài con kiến khác để bảo vệ kiến chúa bằng mọi giá. Đàn chim thực hiện ~q~ lượt tấn công thuộc ~1~ trong ~2~ dạng như sau:

• freeze ~u~: đàn chim chiếm đóng đỉnh ~u~ lại. Khi đó, đàn kiến không thể đi qua đỉnh ~u~. Truy vấn này đảm bảo rằng đỉnh ~u~ phải là một đỉnh không trong trạng thái bị chiếm đóng.
• unfreeze ~u~: dàn chim bỏ chiếm đóng đỉnh ~u~. Khi đó, đàn kiến có thể đi qua đỉnh ~u~. Truy vấn này đảm bảo rằng đỉnh ~u~ phải là một đỉnh đã trong trạng thái bị chiếm đóng.

Sau mỗi lượt, Chovang muốn biết:

• Số lượng cạnh ít nhất cần xóa đi để các đỉnh bị chiếm đóng không thể đến được đỉnh ~1~, điều này giúp cho đàn chim tránh lại gần phòng của kiến chúa.
• Nếu tồn tại nhiều cách xóa cạnh sao cho ít nhất, tìm cách xóa sao cho số lượng đỉnh không bị chiếm đóng mà vẫn không đến được từ đỉnh ~1~ là ít nhất.

Do là phòng của kiến chúa được Chovang bảo vệ rất kỹ nên lũ chim không thể thực hiện thao tác thuộc ~1~ trong ~2~ dạng trên lên đỉnh ~1~.

Input

• Dòng đầu tiên gồm hai số nguyên ~n~ và ~q~ - lần lượt là số căn phòng trong tổ kiến và số lượt tấn công đàn chim thực hiện ~(2 \le n \le 3 \times 10^5),~ ~(1 \le q \le 4 \times 10^5)~
• Dòng thứ hai gồm ~n - 1~ số nguyên, số nguyên ~p_i~ biểu diễn có một cạnh nối giữa nút ~i + 1~ và ~p_i~. ~(1 \le p_i \le n, p_i \ne (i + 1))~
• ~q~ dòng cuối cùng, mỗi dòng có dạng một trong hai thao tác: freeze ~u~ và unfreeze ~u~ ~(1 < u \le n)~

Output

Với mỗi thao tác, ta cần in ra số lượng cạnh ít nhất cần xóa đi để các đỉnh bị chiếm đóng không thể đến được đỉnh ~1~ và số lượng đỉnh ít nhất không bị chiếm đóng mà vẫn không đến được từ đỉnh ~1~.

Sample Input

6 3
1 2 3 3 2
freeze 3
unfreeze 3
freeze 2

Sample Output

1 2
0 0
1 4

Sample Input

7 3
1 2 3 3 2 5
freeze 3
freeze 5
freeze 6

Sample Output

1 3
1 2
1 3

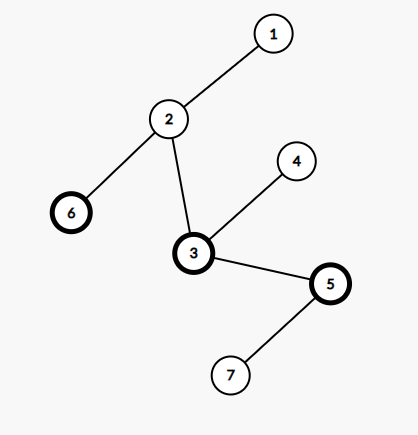
Sample Input

7 2
1 2 3 3 2 5
freeze 5
freeze 6

Sample Output

1 1
1 4

Note

Ở ví dụ thứ nhất, có ~3~ lượt tấn công được thực hiện như sau:

• Lượt thứ ~1~, đàn chim chiếm phòng thứ ~3~, lúc này để ngăn đàn chim thì Chovang xóa đi cạnh nối đỉnh ~2~ với đỉnh ~3~ và có hai đỉnh tuy không bị chiếm nhưng cũng không thể đến được đỉnh ~1~ là đỉnh ~4~ và đỉnh ~5~.

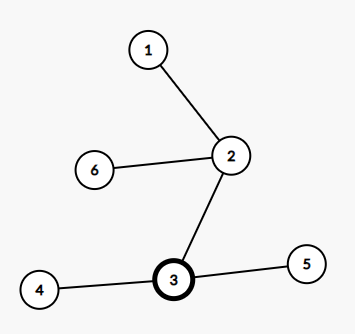
• Lượt thứ ~2~, đàn chim bỏ chiếm phòng thứ ~3~, lúc này Chovang không cần phải xóa đi cạnh nào cả.

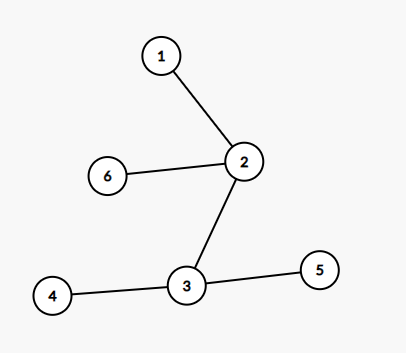
• Lượt thứ ~3~, đàn chim chiếm phòng thứ ~2~, lúc này để ngăn đàn chim thì Chovang xóa đi cạnh nối đỉnh ~1~ với đỉnh ~2~ và có bốn đỉnh tuy không bị chiếm nhưng cũng không thể đến được đỉnh ~1~ là đỉnh ~6~, đỉnh ~3~, đỉnh ~4~ và đỉnh ~5~.

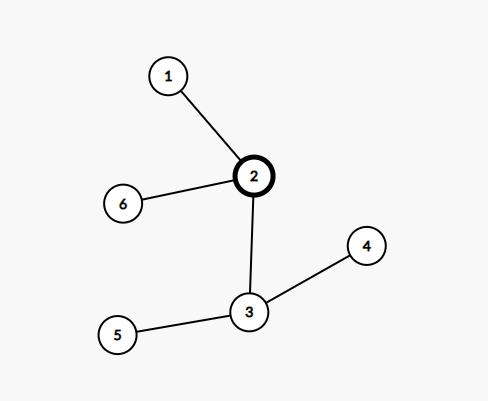
Ở ví dụ thứ hai, có ~3~ lượt tấn công được thực hiện như sau:

• Lượt thứ ~1~, đàn chim chiếm phòng thứ ~3~, lúc này để ngăn đàn chim thì Chovang xóa đi cạnh nối đỉnh ~2~ với đỉnh ~3~ và có ba đỉnh tuy không bị chiếm nhưng cũng không thể đến được đỉnh ~1~ là đỉnh ~4~, đỉnh ~5~ và đỉnh ~7~.

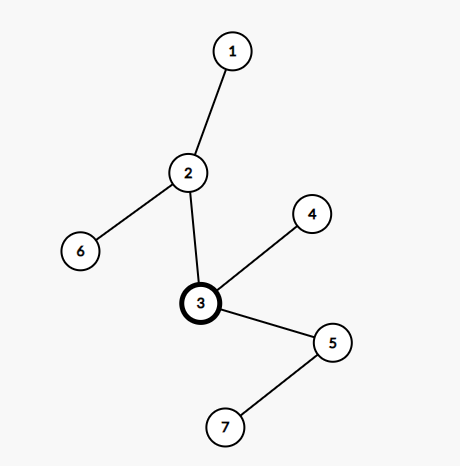
• Lượt thứ ~2~, đàn chim chiếm phòng thứ ~5~, lúc này để ngăn đàn chim thì Chovang có thể xóa đi cạnh nối đỉnh ~2~ với đỉnh ~3~ và cạnh nối đỉnh ~3~ với đỉnh ~5~ nhưng chỉ cần xóa cạnh nối đỉnh ~2~ với đỉnh ~3~ là đủ và cũng là ít nhất, vậy có hai đỉnh tuy không bị chiếm nhưng cũng không thể đến được đỉnh ~1~ là đỉnh ~4~ và đỉnh ~7~.

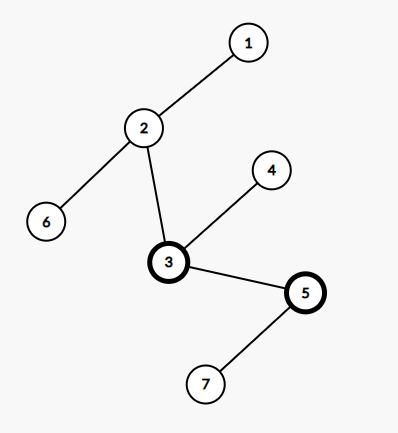
• Lượt thứ ~3~, đàn chim chiếm phòng thứ ~6~, lúc này để ngăn đàn chim thì Chovang xóa đi cạnh nối đỉnh ~1~ với đỉnh ~2~ và có ba đỉnh tuy không bị chiếm nhưng cũng không thể đến được đỉnh ~1~ là đỉnh ~2~, đỉnh ~4~ và đỉnh ~7~.