Bedao Regular Contest 03 - PROTECT
Xem dạng PDFChovang là một dân chơi kiến thực thụ, tổ kiến của Chovang gồm nhiều đàn kiến thợ và một con kiến chúa, thậm chí những con kiến này như một xã hội thu nhỏ mà mỗi con kiến đều có một phòng cho riêng mình. Chovang đã cẩn thận đánh số từng căn phòng cho lũ kiến của mình lần lượt từ ~1~ đến ~n~ mà trong đó phòng thứ ~1~ chính là của kiến chúa. Ta có thể xem tập hợp các căn phòng này là một đồ thị liên thông vô hướng không chu trình gồm ~n~ nút và ~n - 1~ cạnh. Một cạnh là đường đi nối giữa hai căn phòng khác nhau và cả hai căn phòng đều đi qua lại được với nhau từ hai hướng. Ban đầu, tất cả các đỉnh đều có khả năng đi qua nhau được. Đàn kiến có tập tính là hàng ngày đều đi kiếm thức ăn bên ngoài và đem về tổ phục vụ cho kiến chúa, nhưng chẳng may bọn chim đã đánh hơi được một con kiến rồi biết được tổ kiến của Chovang và rất muốn ăn hết từng con kiến trong tổ. Trận chiến nào cũng cần có sự hi sinh nên Chovang chấp nhận sẽ bỏ mặc một vài con kiến khác để bảo vệ kiến chúa bằng mọi giá. Đàn chim thực hiện ~q~ lượt tấn công thuộc ~1~ trong ~2~ dạng như sau:
- freeze ~u~: đàn chim chiếm đóng đỉnh ~u~ lại. Khi đó, đàn kiến không thể đi qua đỉnh ~u~. Truy vấn này đảm bảo rằng đỉnh ~u~ phải là một đỉnh không trong trạng thái bị chiếm đóng.
- unfreeze ~u~: dàn chim bỏ chiếm đóng đỉnh ~u~. Khi đó, đàn kiến có thể đi qua đỉnh ~u~. Truy vấn này đảm bảo rằng đỉnh ~u~ phải là một đỉnh đã trong trạng thái bị chiếm đóng.
Sau mỗi lượt, Chovang muốn biết:
- Số lượng cạnh ít nhất cần xóa đi để các đỉnh bị chiếm đóng không thể đến được đỉnh ~1~, điều này giúp cho đàn chim tránh lại gần phòng của kiến chúa.
- Nếu tồn tại nhiều cách xóa cạnh sao cho ít nhất, tìm cách xóa sao cho số lượng đỉnh không bị chiếm đóng mà vẫn không đến được từ đỉnh ~1~ là ít nhất.
Do là phòng của kiến chúa được Chovang bảo vệ rất kỹ nên lũ chim không thể thực hiện thao tác thuộc ~1~ trong ~2~ dạng trên lên đỉnh ~1~.
Input
- Dòng đầu tiên gồm hai số nguyên ~n~ và ~q~ - lần lượt là số căn phòng trong tổ kiến và số lượt tấn công đàn chim thực hiện ~(2 \le n \le 3 \times 10^5),~ ~(1 \le q \le 4 \times 10^5)~
- Dòng thứ hai gồm ~n - 1~ số nguyên, số nguyên ~p_i~ biểu diễn có một cạnh nối giữa nút ~i + 1~ và ~p_i~. ~(1 \le p_i \le n, p_i \ne (i + 1))~
- ~q~ dòng cuối cùng, mỗi dòng có dạng một trong hai thao tác: freeze ~u~ và unfreeze ~u~ ~(1 < u \le n)~
Output
Với mỗi thao tác, ta cần in ra số lượng cạnh ít nhất cần xóa đi để các đỉnh bị chiếm đóng không thể đến được đỉnh ~1~ và số lượng đỉnh ít nhất không bị chiếm đóng mà vẫn không đến được từ đỉnh ~1~.
Sample Input
6 3
1 2 3 3 2
freeze 3
unfreeze 3
freeze 2
Sample Output
1 2
0 0
1 4
Sample Input
7 3
1 2 3 3 2 5
freeze 3
freeze 5
freeze 6
Sample Output
1 3
1 2
1 3
Sample Input
7 2
1 2 3 3 2 5
freeze 5
freeze 6
Sample Output
1 1
1 4
Note
Ở ví dụ thứ nhất, có ~3~ lượt tấn công được thực hiện như sau:
- Lượt thứ ~1~, đàn chim chiếm phòng thứ ~3~, lúc này để ngăn đàn chim thì Chovang xóa đi cạnh nối đỉnh ~2~ với đỉnh ~3~ và có hai đỉnh tuy không bị chiếm nhưng cũng không thể đến được đỉnh ~1~ là đỉnh ~4~ và đỉnh ~5~.
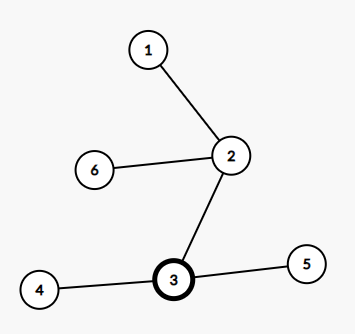
- Lượt thứ ~2~, đàn chim bỏ chiếm phòng thứ ~3~, lúc này Chovang không cần phải xóa đi cạnh nào cả.
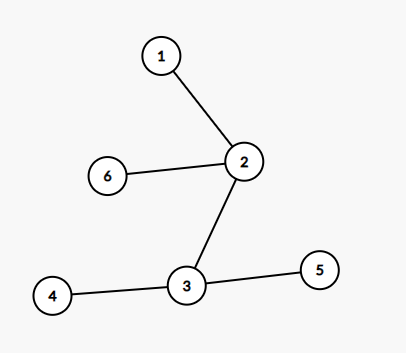
- Lượt thứ ~3~, đàn chim chiếm phòng thứ ~2~, lúc này để ngăn đàn chim thì Chovang xóa đi cạnh nối đỉnh ~1~ với đỉnh ~2~ và có bốn đỉnh tuy không bị chiếm nhưng cũng không thể đến được đỉnh ~1~ là đỉnh ~6~, đỉnh ~3~, đỉnh ~4~ và đỉnh ~5~.
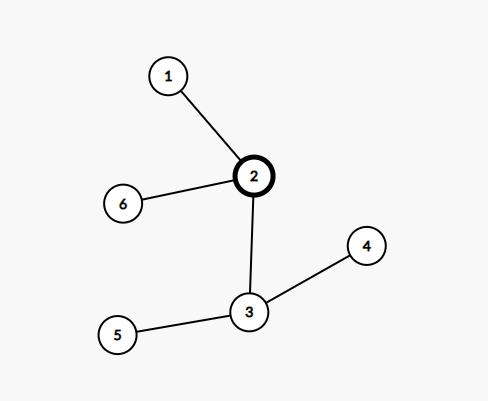
Ở ví dụ thứ hai, có ~3~ lượt tấn công được thực hiện như sau:
- Lượt thứ ~1~, đàn chim chiếm phòng thứ ~3~, lúc này để ngăn đàn chim thì Chovang xóa đi cạnh nối đỉnh ~2~ với đỉnh ~3~ và có ba đỉnh tuy không bị chiếm nhưng cũng không thể đến được đỉnh ~1~ là đỉnh ~4~, đỉnh ~5~ và đỉnh ~7~.
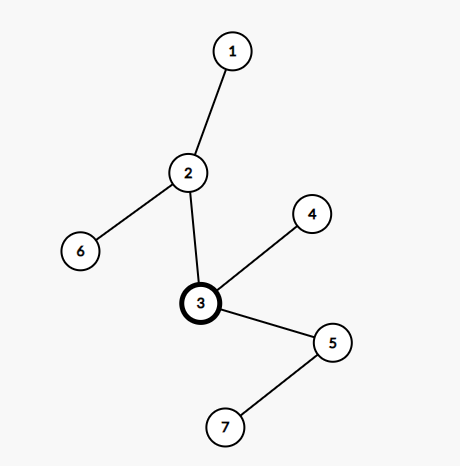
- Lượt thứ ~2~, đàn chim chiếm phòng thứ ~5~, lúc này để ngăn đàn chim thì Chovang có thể xóa đi cạnh nối đỉnh ~2~ với đỉnh ~3~ và cạnh nối đỉnh ~3~ với đỉnh ~5~ nhưng chỉ cần xóa cạnh nối đỉnh ~2~ với đỉnh ~3~ là đủ và cũng là ít nhất, vậy có hai đỉnh tuy không bị chiếm nhưng cũng không thể đến được đỉnh ~1~ là đỉnh ~4~ và đỉnh ~7~.
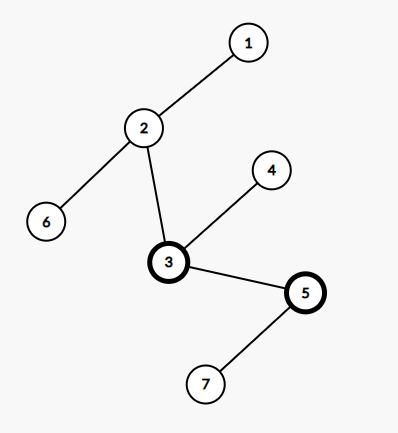
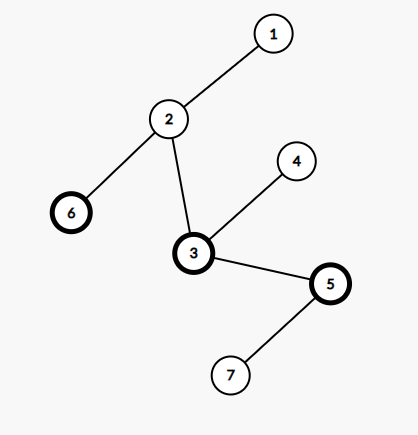
- Lượt thứ ~3~, đàn chim chiếm phòng thứ ~6~, lúc này để ngăn đàn chim thì Chovang xóa đi cạnh nối đỉnh ~1~ với đỉnh ~2~ và có ba đỉnh tuy không bị chiếm nhưng cũng không thể đến được đỉnh ~1~ là đỉnh ~2~, đỉnh ~4~ và đỉnh ~7~.

Bình luận