Giới thiệu về Centroid Decomposition
đã đăng vào 1, Tháng 11, 2021, 14:21Outline
- Lời nói đầu
- Trọng tâm là gì?
- Cách tìm trọng tâm
- Centroid Decomposition
- Centroid Decompsition là gì?
- Cài đặt
- Một số tính chất
- Ví dụ
- CF342E - Xenia and Tree
- IOI'11 - Race
- Thêm
- Tham khảo
Lời nói đầu
Đầu tiên xin cảm ơn bạn Robert (github: https://robert1003.github.io/) đã cho phép và giúp đỡ mình tạo nên blog này.
English: Firstly thanks Robert (github: https://robert1003.github.io/) for allowing and helping me to create this blog.
Chào mọi người. Đây là lần đầu tiên mình viết blog (dù là blog dịch của bạn khác) và cũng là lần đầu tiên mình dịch blog nước ngoài. Có thể trong lúc dịch câu cú không hợp lý mong mọi người thông cảm. Bên cạnh đó các bạn có thể đọc nguyên văn Tiếng Anh của blog tại đây.
Mục đích viết blog của mình là muốn giao lưu chia sẻ với cộng đồng VNOI users và phát triển một cộng đồng vững mạnh. Một lý do khác nữa là bên VNOI wiki chưa có bài viết về chủ đề này nên mình nghĩ một số bạn (như mình) sẽ cần đến. So hope you guys enjoy!
Trọng tâm là gì?
Cho cây ~T~ gồm ~n~ đỉnh. Đỉnh ~u~ được gọi là trọng tâm (Centroid) nếu kích thước của mỗi cây con sau khi xóa ~u~ đều không lớn hơn ~\frac{n}{2}~. Lưu ý rằng trung tâm của cây (thường liên quan đến độ cao cây đó) khác với trọng tâm của cây.
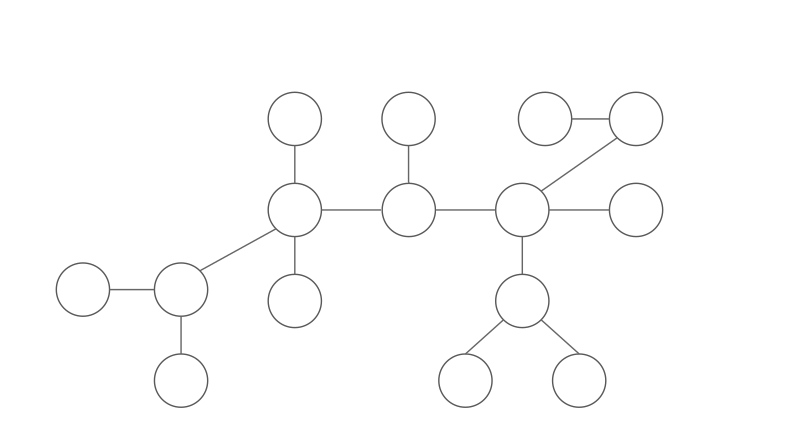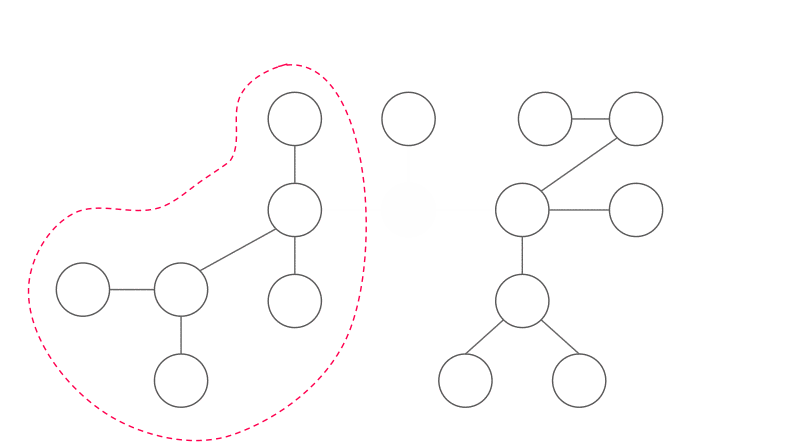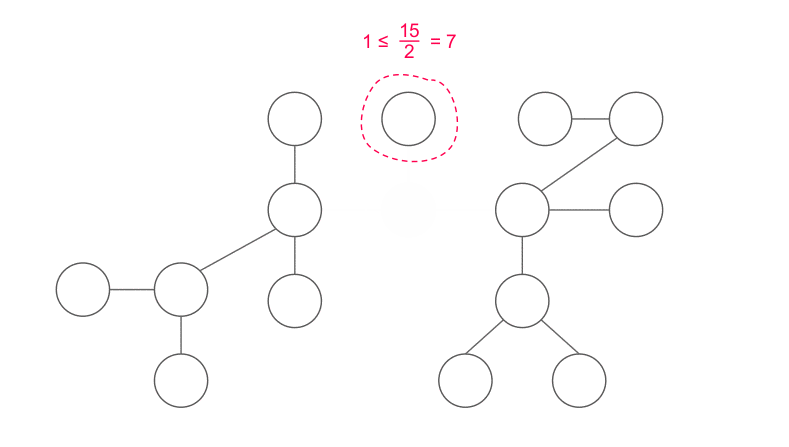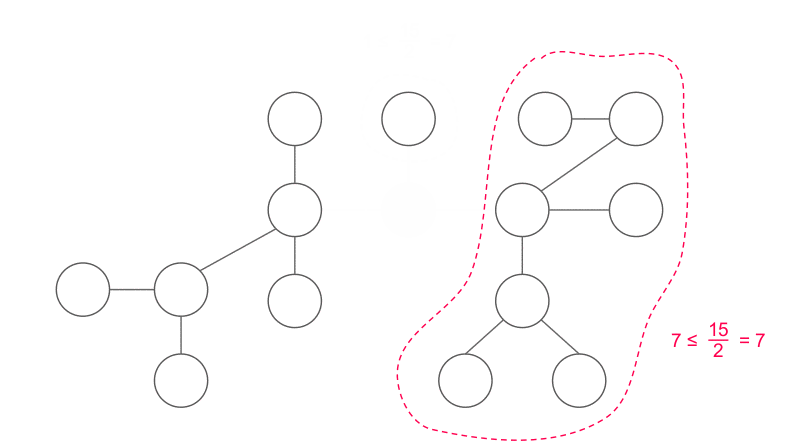
Cách tìm trọng tâm
Đầu tiên, chọn đỉnh ~x~ bất kì. Ta sử dụng DFS để tính kích thước của mỗi cây con (~x~ là gốc). Sau đó, ta có thể "đi" đến trọng tâm từ ~x~ bằng cách:
- Nếu ~x~ là trọng tâm, trả về ~x~.
- Nếu không, ta biết rằng tồn tại duy nhất một đỉnh ~y~ kề ~x~ thỏa mãn ~|y| > \frac{n}{2}~. Di chuyển tới ~y~ và lặp lại.
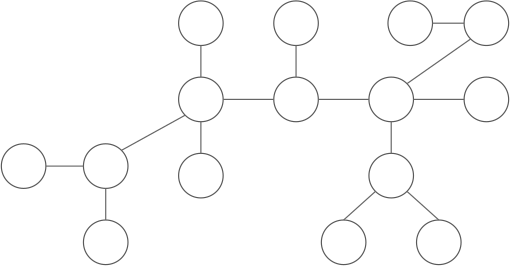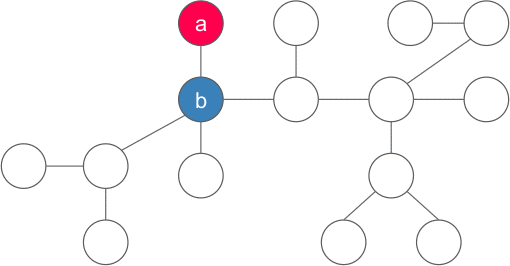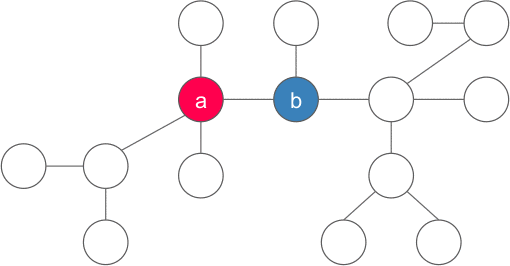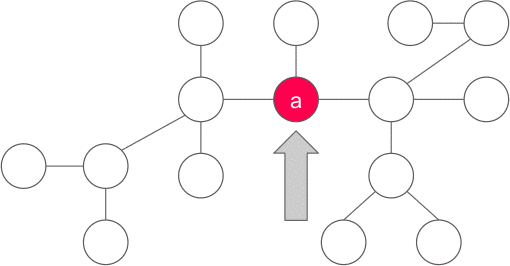
~|y|~ là số lượng đỉnh nằm trong cây con gốc ~y~. Vì sao chỉ có duy nhất một ~y~ thỏa mãn? Luôn tồn tại ít nhất một đỉnh như vậy vì ~x~ không phải là trọng tâm, và tồn tại nhiều nhất một đỉnh như vậy vì nếu hai hoặc nhiều đỉnh như thế sẽ khiến ~|x| > n~.
vector<int> G[N]; // tree stored in adjacency list
int sz[N];
int dfs(int u, int p) {
sz[u] = 1;
for(auto v : G[u]) if(v != p) {
sz[u] += dfs(v, u);
}
return sz[u];
}
int centroid(int u, int p, int n) { // n is the size of tree
for(auto v : G[u]) if(v != p) {
if(sz[v] > n / 2) return centroid(v, u, n);
}
return u;
}
Độ phức tạp là ~O(n)~.
Centroid Decomposition
Kĩ thuật này thực chất là Chia để trị trên cây.
Centroid Decomposition là gì?
Centroid Decomposition của cây ~T~ là một cây ~T'~ được định nghĩa một cách đệ quy như sau:
- Gốc của ~T'~ là trọng tâm của ~T~.
- Con của gốc là trọng tâm của các cây con sau khi xóa trọng tâm của ~T~.
Quá khó hiểu? Hãy xem qua ví dụ sau:
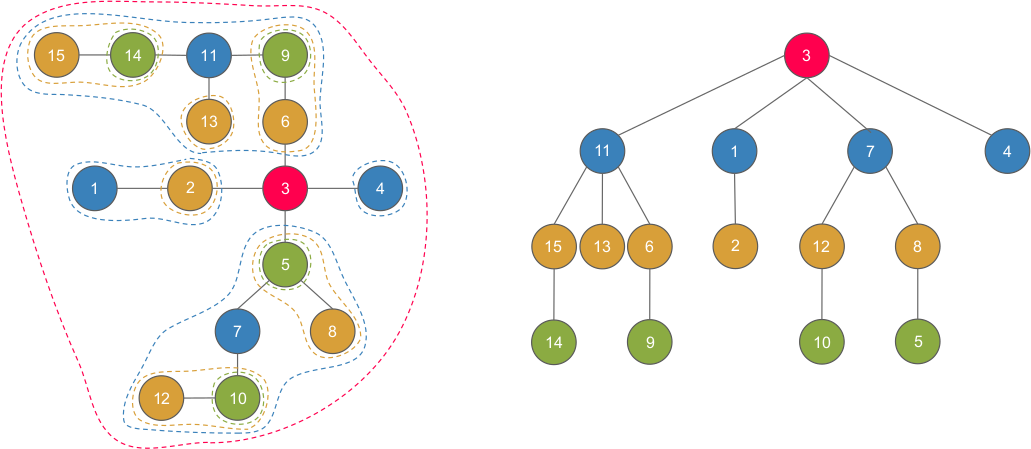
- ~3~ là gốc của cây centroid, và trọng tâm của các cây con sau khi xóa ~3~ trong cây ban đầu gồm ~11, 1, 7, 4~ là con của ~3~.
- ~11~ là gốc của cây centroid, và trọng tâm của các cây con sau khi xóa ~11~ trong cây ban đầu gồm ~15, 13, 6~ là con của ~11~.
~...~ và tiếp tục như vậy.
Cài đặt
set<int> G[N]; // adjacency list (note that this is stored in set, not vector)
int sz[N], pa[N];
int dfs(int u, int p) {
sz[u] = 1;
for(auto v : G[u]) if(v != p) {
sz[u] += dfs(v, u);
}
return sz[u];
}
int centroid(int u, int p, int n) {
for(auto v : G[u]) if(v != p) {
if(sz[v] > n / 2) return centroid(v, u, n);
}
return u;
}
void build(int u, int p) {
int n = dfs(u, p);
int c = centroid(u, p, n);
if(p == -1) p = c;
pa[c] = p;
vector<int> tmp(G[c].begin(), G[c].end());
for(auto v : tmp) {
G[c].erase(v); G[v].erase(c);
build(v, c);
}
}
Xây dựng các cấp bậc của cây centroid chi phí ~O(n)~, chiều cao của cây là ~O(\log n)~. Chi phí xóa cạnh là ~O(n \log n)~, vì ta chỉ có ~O(n)~ cạnh để xóa và chi phí xóa là ~O(\log n)~. Vì vậy, tổng độ phức tạp là ~O(n \log n)~.
Một số tính chất
- Đỉnh ~u~ nằm trong thành phần của tất cả các tổ tiên của nó.
- Đường đi từ ~u~ đến ~v~ có thể tách thành đường đi từ ~u~ đến ~w~, từ ~w~ đến ~v~ với ~w~ là tổ tiên chung gần nhất của ~u~, ~v~ trên cây centroid.
- Ta có thể biểu diễn mọi đường đi hợp lệ trên cây ban đầu (có ~n^2~ đường đi) thành sự kết hợp của ~O(n \log n)~ tập các đường như sau: ~(u, fa(u)), (u, fa(fa(u))), ...~ với mọi ~u~.
Ví dụ minh họa

- Nhìn vào ~9~. Ta có thể thấy rằng ~9~ nằm trong thành phần của các tổ tiên ~6, 11, 3~.
- Lấy ví dụ ~14~ và ~10~ ⟹ ~path(14, 10) = path(14, 3) + path(3, 10)~, với ~3 = lca(14, 10)~.
- "Tập ~O(n \log n)~" cạnh (trên cây centroid) như ~(14, 15), (14, 11), (14, 3)~ và ~(13, 11), (13, 3)~ vân vân. Bây giờ chọn một đường bất kì, ví dụ như ~(1, 4)~. Khi đó ~(1, 4) = (1, 3) + (4, 3)~, là hai cạnh có trong tập đó.
Chứng minh
- Dựa vào cách xây dựng cây centroid.
- Phương pháp phản chứng: Giả sử ~w = lca(u, v)~ không phải là đường từ ~u~ đến ~v~. Từ đó thấy rằng ~u, v~ thuộc cùng một cây con khi loại bỏ ~w~. Tuy nhiên, điều đó nghĩa là ~lca(u, v)~ không phải là ~w~ ⟹ Mâu thuẫn.
- Trước tiên, vì độ cao của cây centroid là ~O(\lg n)~, kích thước của tập đó sẽ là ~O(n \lg n)~. Sau đó, theo tính chất thứ hai, mọi đường đi đều có thể tách thành hai phần, và phân tách ở chính lca của chúng. Do đó, mọi đường đi đều có thể biểu diễn bằng các phần tử trong tập đó.
Ví dụ
CF342E - Xenia and Tree
Tóm tắt
Bạn được cho một cây gồm ~N~ đỉnh, đánh số từ ~1~ đến ~N~. Mọi đỉnh đều được tô bởi màu đỏ hoặc xanh. Ban đầu, đỉnh ~1~ màu đỏ, và mọi đỉnh khác màu xanh. Bây giờ, bạn cần xử lí ~Q~ truy vấn thuộc một trong hai dạng sau:
- ~1\: u~: Tô đỉnh ~u~ từ màu xanh sang màu đỏ.
- ~2\: u~: Tìm chỉ số của đỉnh màu đỏ gần ~u~ nhất.
~2 \le N \le 10^5, 1 \le Q \le 10^5~
Phân tích
Trước hết, ta nhận thấy rằng câu trả lời cho truy vấn loại ~2~ yêu cầu xử lí toàn bộ đường đi bắt đầu từ ~u~, với chi phí ~O(N)~ nếu giải quyết "ngây thơ". Bây giờ, xem lại tính chất ~3~ của centroid decomposition. Tính chất này cho thấy nếu ta muốn lấy thông tin của đường đi bằng cách "hợp" hai phần của đường, thì ta có thể trả lời truy vấn loại ~2~ trong ~O(\lg N)~.
Lời giải
Với mỗi đỉnh ~u~, ta duy trì giá trị ~ans_u = \min_{v\,is\,red,\, v \,∈\,centroid\,tree\,rooted\,at\,u}dis(u, v)~, khoảng cách của đỉnh màu đỏ gần nhất tới ~u~ xét các đỉnh trong thành phần mà ~u~ là trọng tâm. Sau đó, ta có thể xử lí truy vấn bằng cách:
- Tô màu: cập nhật giá trị ans của tất cả các tổ tiên của ~u~, nghĩa là, ~ans_v = \min(ans_v, dis(u, v))~ với mọi ~v ∈~ tổ tiên của ~u~.
- Truy vấn: ~\min_{v \,∈\, ancestors \, of \, u}(ans_v + dis(u, v))~ là kết quả.
Cả hai truy vấn đều ~O(\log N)~, vì độ cao của cây centroid tối đa là ~O(\log N)~. Vì vậy, độ phức tạp tổng quát là ~O(Q \log N)~.
Code
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = (int)1e5 + 5; const int inf = (int)1e9; struct CentroidDecomposition { set<int> G[N]; map<int, int> dis[N]; int sz[N], pa[N], ans[N]; void init(int n) { for(int i = 1 ; i <= n ; ++i) G[i].clear(), dis[i].clear(), ans[i] = inf; } void addEdge(int u, int v) { G[u].insert(v); G[v].insert(u); } int dfs(int u, int p) { sz[u] = 1; for(auto v : G[u]) if(v != p) { sz[u] += dfs(v, u); } return sz[u]; } int centroid(int u, int p, int n) { for(auto v : G[u]) if(v != p) { if(sz[v] > n / 2) return centroid(v, u, n); } return u; } void dfs2(int u, int p, int c, int d) { // build distance dis[c][u] = d; for(auto v : G[u]) if(v != p) { dfs2(v, u, c, d + 1); } } void build(int u, int p) { int n = dfs(u, p); int c = centroid(u, p, n); if(p == -1) p = c; pa[c] = p; dfs2(c, p, c, 0); vector<int> tmp(G[c].begin(), G[c].end()); for(auto v : tmp) { G[c].erase(v); G[v].erase(c); build(v, c); } } void modify(int u) { for(int v = u ; v != 0 ; v = pa[v]) ans[v] = min(ans[v], dis[v][u]); } int query(int u) { int mn = inf; for(int v = u ; v != 0 ; v = pa[v]) mn = min(mn, ans[v] + dis[v][u]); return mn; } } cd; int n, q; void init() { cin >> n >> q; cd.init(n); for(int i = 0 ; i < n - 1 ; ++i) { int a, b; cin >> a >> b; cd.addEdge(a, b); } cd.build(1, 0); } void solve() { cd.modify(1); int t, u; while(q--) { cin >> t >> u; if(t == 1) cd.modify(u); else cout << cd.query(u) << '\n'; } } int main() { ios_base::sync_with_stdio(0), cin.tie(0); init(); solve(); }
IOI'11 - Race
Tóm tắt
Bạn được cho một cây có trọng số gồm ~N~ đỉnh, đánh số từ ~1~ đến ~N~. Tìm đường đi độ dài ~K~ sử dụng ít cạnh nhất hoặc xuất ra "~-1~" nếu đường đi đó không tồn tại.
~1\le N \le 2 \times 10^5, 1 \le w_{i, j} \in \mathbb{N} \le 10^6, 1 \le K \le 10^6~.
Phân tích
Giống với bài toán trước, ta cần xử lí toàn bộ đường đi. Tuy nhiên, trong bài toán này, thay vì cực tiểu hóa độ dài đường đi, ta cần phải tìm giá trị đặc trưng của đường đi trong khi cực tiểu hóa số cạnh. Để ý rằng centroid decomposition là thuật toán D&C. Hãy thử giải quyết bài toán sử dụng đến nó. Phần chia rất dễ dàng, chỉ cần lấy đáp án trên cây con (sau khi loại bỏ trọng tâm). Với phần hợp, ta cần xử lí đường đi đi qua trọng tâm hiện tại. Ta có thể sử dụng DFS để tính khoảng cách từ trọng tâm đến các nút con của nó. Sau đó, dùng một DFS khác để lấy kết quả.
Lời giải
Đầu tiên, ta dùng centroid decomposition trên cây. Gọi ~u~ là trọng tâm của cây. Sau đó, lấy kết quả bằng thuật toán sau:
Solve(u):
ans = inf
for v là con u:
ans = min(ans, Solve(v))
DFS từ u để tính khoảng cách và số cạnh đã sử dụng trong thành phần của u
Sử dụng DFS khác để tính kết quả, trong khi sử dụng một mảnh để truy vết các đường đi thỏa mãn bắt đầu từ
u và số cạnh cần dùng ít nhất
cập nhật ans từ hàm DFS trước
return ans
Độ phức tạp là ~O(N \log N)~.
Code
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = (int)2e5 + 5; const int M = (int)1e6 + 5; const int inf = (int)1e9; set<pair<int, int> > G[N]; int n, k, sz[N], exist[M], edgecnt[M], tt; int dfs(int u, int p) { sz[u] = 1; for(auto it : G[u]) if(it.first != p) { sz[u] += dfs(it.first, u); } return sz[u]; } int centroid(int u, int p, int nn) { for(auto it : G[u]) if(it.first != p) { if(sz[it.first] > nn / 2) return centroid(it.first, u, nn); } return u; } int dfs2(int u, int p, int d, int cnt, int t, vector<pair<int, int> >& v) { int want = k - d, ans = inf; if(want >= 0 && exist[want] == t) { ans = min(ans, cnt + edgecnt[want]); } if(d <= k) { v.push_back({d, cnt}); for(auto it : G[u]) if(it.first != p) { ans = min(ans, dfs2(it.first, u, d + it.second, cnt + 1, t, v)); } } return ans; } int Solve(int u, int p) { int nn = dfs(u, p); int c = centroid(u, p, nn); int ans = inf; int t = ++tt; exist[0] = t; edgecnt[0] = 0; for(auto it : G[c]) { // dfs one subtree at a time vector<pair<int, int> > tmp; ans = min(ans, dfs2(it.first, c, it.second, 1, t, tmp)); for(auto itt : tmp) { if(exist[itt.first] != t || (exist[itt.first] == t && edgecnt[itt.first] > itt.second)) { exist[itt.first] = t; edgecnt[itt.first] = itt.second; } } } vector<pair<int, int> > tmp(G[c].begin(), G[c].end()); for(auto it : tmp) { G[c].erase(it); G[it.first].erase({c, it.second}); ans = min(ans, Solve(it.first, c)); } return ans; } void init() { cin >> n >> k; for(int i = 1 ; i < n ; ++i) { int u, v, w; cin >> u >> v >> w; G[u].insert({v, w}); G[v].insert({u, w}); } } void solve() { tt = 0; int ans = Solve(0, -1); cout << (ans == inf ? -1 : ans) << '\n'; } int main() { ios_base::sync_with_stdio(0), cin.tie(0); init(); solve(); }
Thêm
- Codechef - Count It
- Đây là danh sách các bài có thể giải bằng centroid decomposition. Chúc các bạn vui vẻ!