Ngắm sao
Xem dạng PDFChíp có sở thích ngắm sao vào mỗi buổi đêm. Đêm nay, trời đặc biệt đầy sao. Chíp đếm được có ~N~ ngôi sao trên trời, Chíp ghi nhớ mỗi ngôi sao và đánh số chúng từ ~1~ đến ~N~. Mỗi ngôi sao được biểu diễn bằng một đường tròn trên mặt phẳng tọa độ, ngôi sao thứ ~i~ có tâm nằm ở tọa độ ~(A_i~, ~B_i)~ và bán kính ~R_i~. Những ngôi sao có thể đè lên nhau.
Chíp đứng ở trên mặt đất, tức là trục hoành, và nhìn thẳng lên trời. Chíp muốn biết ngôi sao gần nhất mà mình nhìn thấy được là ngôi sao nào, để có thể chọn chỗ đứng thích hợp ngắm ngôi sao mình thích. Vì vậy, Chíp đặt ra ~Q~ câu hỏi, mỗi câu hỏi gồm một số ~X_i~, hỏi rằng nếu đứng ở vị trí ~(X_i~, ~0)~ thì ngôi sao gần nhất Chíp nhìn thấy là ngôi sao nào.
Tại vị trí ~(X_i~, ~0)~, vẽ một tia song song và cùng chiều với trục tung, đường tròn đầu tiên nó chạm vào thì ngôi sao tương ứng với đường tròn đó là ngôi sao đầu tiên Chíp nhìn thấy. Bạn hãy giúp Chíp trả lời ~Q~ câu hỏi này nhé.
Input
- Dòng đầu tiên gồm hai số nguyên ~N~, ~Q~ ~(1 \leq N~, ~Q \leq 50000)~.
- ~N~ dòng tiếp theo, dòng thứ ~i~ gồm ba số nguyên ~A_i~, ~B_i~, ~R_i~ mô tả ngôi sao thứ ~i~.
- ~Q~ dòng tiếp theo, dòng thứ ~i~ gồm một số nguyên ~X_i~ mô tả truy vấn thứ ~i~.
- ~(1 \leq A_i~, ~B_i~, ~R_i~, ~X_i \leq 10^5~, ~B_i>R_i)~.
Output
- In ra ~Q~ dòng, mỗi dòng gồm một số nguyên là chỉ số ngôi sao gần nhất Chíp nhìn thấy nếu đứng ở ~(X_i~, ~0)~.
- Nếu nhìn thấy được nhiều ngôi sao gần nhất thì in ra chỉ số của ngôi sao có chỉ số nhỏ nhất.
- Nếu tại vị trí đó nhìn thẳng lên không có ngôi sao nào thì in ra ~-1~.
Sample Input
4 5
2 3 2
6 9 2
5 5 2
4 7 3
4
7
8
1
9
Sample Output
1
3
2
1
-1
Note
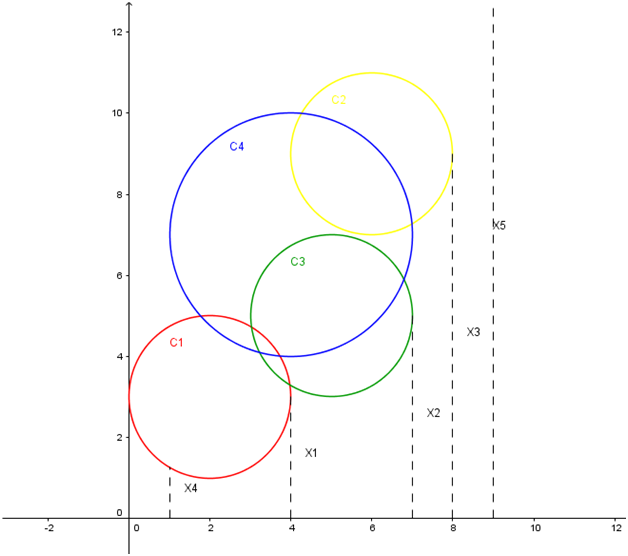
Bình luận
Hướng làm của mình