Mùa Giáng Sinh năm nay ấm áp, đôi bạn Đông và Bắc rủ nhau ở nhà cùng nghiên cứu một thuật toán sắp xếp tổ hợp có cấu trúc đặc biệt. Ban đầu Đông chuẩn bị một hoán vị ~\pi =~ (~\pi_1~, ~\pi_2~, ..., ~\pi_n~) của ~n~ số nguyên dương ~1~, ~2~, ..., ~n~ rồi đưa cho Bắc. Tiếp theo, Đông tìm hoán vị đi ngay sau hoán vị ~\pi~ trong thứ tự từ điển rồi đưa cho Bắc, và cứ tiếp tục như vậy. Nhắc lại là: Hoán vị ~ρ~ = (~ρ_1~, ~ρ_2~, ..., ~ρ_n~) được gọi là đi trước hoán vị ~σ = (σ_1~, ~σ_2~, ..., ~σ_n~) theo thứ tự từ điển nếu như tồn tại một chỉ số ~i~ (~1 \leq i \leq n~) sao cho:

• nếu ~i = 1~ thì ~ρ_i < σ_i~;
• nếu ~1 < i \leq n~ thì ~ρ_j = σ_j~ với ~j < i~ và ~ρ_i < σ_i~.

Với mỗi hoán vị ~\pi~ nhận được từ Đông, Bắc tiến hành dựng cây nhị phân ~T~ (~\pi~) có cấu trúc như sau:

• Nút gốc của ~T~ (~\pi~) được gán nhãn ~n~ là số lớn nhất của ~\pi~;
• Giả sử ~\pi^{left}~ và ~\pi^{right}~ lần lượt là dãy con bên trái và bên phải của ~n~ trong ~\pi~. Gọi ~a~ là số lớn nhất của dãy ~\pi^{left}~ và ~b~ là số lớn nhất của dãy ~\pi^{right}~. Khi đó nút gốc của ~T~ (~\pi~) sẽ có hai cây con: cây con trái ~T~ (~\pi^{left}~) với gốc được gán nhãn ~a~ và cây con phải ~T~ (~\pi^{right}~) với gốc được gán nhãn ~b~. Nếu dãy ~\pi^{left}~ là rỗng thì nút gốc của ~T~ (~\pi~) không có con trái. Nếu dãy ~\pi^{right}~ là rỗng thì nút gốc của ~T~ (~\pi~) không có con phải;
• Nếu dãy ~\pi^{left}~ là khác rỗng thì cây con ~T~ (~\pi^{left}~) gốc tại ~a~ được xây dựng một cách đệ qui đối với dãy con ~\pi^{left}~ giống như việc xây dựng cây ~T~ (~\pi~);
• Nếu dãy ~\pi^{right}~ là khác rỗng thì cây con ~T~ (~\pi^{right}~) gốc tại ~b~ được xây dựng một cách đệ qui đối với dãy con ~\pi^{right}~ giống như việc xây dựng cây ~T~ (~\pi~).

Vídụ: Với ~\pi =~ (~2~, ~6~, ~3~, ~4~, ~9~, ~8~, ~1~, ~7~, ~5~) thì cây ~T~ (~\pi~) được mô tả như trong hình ~1~.

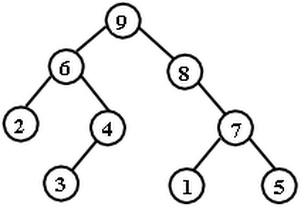
Hình ~1~. Cây ~T~ (~\pi~) tương ứng với hoán vị ~\pi =~ (~2~, ~6~, ~3~, ~4~, ~9~, ~8~, ~1~, ~7~, ~5~)

Cây ~T~ (~\pi~) xây dựng theo qui tắc nêu trên được gọi là cây nhị phân tương ứng với hoán vị ~\pi~.

Tiếp theo Bắc tiến hành liệt kê các nút của cây ~T~ (~\pi~) theo thứ tự sau và thu được một hoán vị mới gồm các nhãn của các nút được sắp xếp theo trình tự các nút được liệt kê. Nhắc lại là: Việc liệt kê các nút của cây ~T~ (~\pi~) theo thứ tự sau được định nghĩa một cách đệ qui như sau:

• Nếu cây ~T~ (~\pi~) chỉ có một nút thì danh sách gồm một nút duy nhất đó là danh sách các nút của cây ~T~ (~\pi~) được liệt kê theo thứ tự sau;
• Nếu cây ~T~ (~\pi~) có nhiều hơn một nút thì danh sách các nút của cây ~T~ (~\pi~) được liệt kê theo thứ tự sau là: đầu tiên là các nút của cây con trái của ~T~ (~\pi~) được liệt kê theo thứ tự sau, tiếp đến là các nút của của cây con phải của ~T~ (~\pi~) được liệt kê theo thứ tự sau, cuối cùng là nút gốc.

Ví dụ: Với hoán vị trong ví dụ trên, hoán vị thu được bởi việc liệt kê các nút của cây nhị phân tương ứng với nó ~T~ (~\pi~) theo thứ tự sau là (~2~, ~3~, ~4~, ~6~, ~1~, ~5~, ~7~, ~8~, ~9~).

Đôi bạn xét tính chất TSort sau đây trên tập các hoán vị của các số nguyên dương từ ~1~ đến ~n~: "Hoánvị ~\pi~ được nói là có tính chất TSort nếu việc liệt kê các nút của cây nhị phân tương ứng với nó ~T~ (~\pi~) theo thứ tự sau cho ta hoán vị đơn vị, nghĩa là hoán vị có dạng (~1~, ~2~, ..., ~n~)". Đông và Bắc muốn khảo sát xem những hoán vị như vậy có phải là thường gặp hay không.

Yêu cầu: Cho ~\pi~ là một hoán vị của các số ~1~, ~2~, ..., ~n~, hãy viết chương trình giúp đôi bạn xác định số lượng hoán vị trong số ~k~ hoán vị liên tiếp theo thứ tự từ điển bắt đầu từ ~\pi~ (kể cả ~\pi~) thoả mãn tính chất TSort.

Input

• Dòng đầu gồm hai số nguyên dương ~n~ và ~k~;
• Dòng thứ hai gồm ~n~ số nguyên dương ~\pi_1~, ~\pi_2~, ..., ~\pi_n~ là các thành phần của hoán vị ~\pi~. Hai số liên tiếp trên cùng một dòng được ghi cách nhau bởi dấu cách.

Output

• Ghi ra một số nguyên duy nhất là số lượng hoán vị trong số ~k~ hoán vị liên tiếp theo thứ tự từ điển bắt đầu từ ~\pi~ (kể cả ~\pi~) thoả mãn tính chất TSort.

Giới hạn

• Có 30% số test tương ứng với các bộ dữ liệu có giới hạn ~n~, ~k \leq 100~;
• Có 30% số test khác tương ứng với các bộ dữ liệu có giới hạn ~n~, ~k \leq 10^{3}~;
• Có 40% số test còn lại tương ứng với các bộ dữ liệu có giới hạn ~n \leq 10^{3}~, ~k \leq 10^{6}~.

Sample Input

4 6
1 3 4 2

Sample Output

4