VOI 26 Bài 6 - Cắm trại
Xem dạng PDFVào năm mới, ~K~ gia đình tổ chức cắm trại trên một khu đất có dạng hình tròn. Khu đất được biểu diễn trên hệ trục tọa độ Đề-các ~Oxy~ (đơn vị mét), có tâm ở gốc tọa độ ~O(0,0)~ và bán kính ~R = 100~ mét. Trên biên hình tròn, chọn ~K~ điểm phân biệt để làm vị trí cắm trại cho ~K~ gia đình. Các điểm được đánh số từ ~1~ đến ~K~ và được xác định bằng dãy góc ~\alpha_1, \alpha_2, \ldots, \alpha_K~ (~0^\circ \le \alpha_1 < \alpha_2 < \ldots < \alpha_K \le 359^\circ~), ~\alpha_i~ là góc từ tia ~Ox~ ngược chiều kim đồng hồ tới tia nối ~O~ đến điểm thứ ~i~. Cụ thể, điểm thứ ~i~ (~1 \le i \le K~) có tọa độ là ~\left( R \times \cos \frac{\alpha_i \times \pi}{180^\circ}, R \times \sin\frac{\alpha_i \times \pi}{180^\circ} \right)~, trong bài toán này lấy ~\pi = 3.14159265359~.
Alice nhận nhiệm vụ thiết kế đường dây để cấp điện cho tất cả các trại. Cụ thể, máy phát điện đặt ở trại ~1~, cần kết nối trại ~1~ tới ~K-1~ trại còn lại bằng dây điện. Trong quá trình thiết kế, được phép thêm tối đa ~25~ điểm trung gian để đấu nối nhưng các điểm này phải nằm trong hoặc trên biên của mảnh đất hình tròn. Các dây điện có thể đấu nối giữa hai trại, giữa một trại với một điểm trung gian, giữa hai điểm trung gian. Độ dài dây điện nối trực tiếp giữa hai điểm có tọa độ ~(x_1, y_1)~ và ~(x_2,y_2)~ là ~\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}~. Cần thiết kế sao cho với một trại bất kỳ, tồn tại duy nhất một đường dẫn điện trực tiếp hoặc gián tiếp từ trại ~1~ tới trại đó. Giả sử phần dây hao hụt trong quá trình đấu nối là không đáng kể.
Alice đã thiết kế được một phương án có tổng độ dài dây điện sử dụng là ~A~ mét. Cô đã mua đúng ~A~ mét dây điện. Tuy nhiên chưa kịp triển khai thì bản vẽ bị mất. Alice nhờ Bob thiết kế lại một phương án, nếu phương án của Bob có tổng độ dài dây điện cần dùng lớn hơn ~A~ thì họ phải mua thêm cho đủ, ngược lại thì không cần mua thêm.
Yêu cầu: Hãy giúp Bob tìm cách thiết kế sao cho tổng độ dài dây điện cần mua thêm là càng nhỏ càng tốt.
Input
Vào từ file văn bản ~\texttt{CAMP.INP}~:
Dòng đầu chứa một số nguyên dương ~K~ (~3 \le K \le 10~).
Dòng thứ hai chứa ~K~ số nguyên không âm ~\alpha_1, \alpha_2, \ldots, \alpha_K~.
Dòng cuối cùng ghi số thực ~A~ (~0 < A < 2 \times \pi \times R~).
Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra file văn bản ~\texttt{CAMP.OUT}~:
Dòng đầu ghi một số tự nhiên ~M~ là số lượng điểm trung gian (~0 \le M \le 25~).
Nếu ~M > 0~ thì ~M~ điểm này được đánh số thứ tự từ ~K+1~ đến ~K+M~, và ghi ra ~M~ dòng tiếp theo, dòng thứ ~i~ chứa hai số thực là tọa độ của điểm thứ ~K+i~. Các giá trị tọa độ được ghi ra với độ chính xác đến bốn chữ số sau dấu chấm thập phân.
Mỗi dòng trong số ~K + M - 1~ dòng tiếp theo ghi hai số nguyên dương ~u~ và ~v~, mô tả một dây điện nối giữa điểm thứ ~u~ và điểm thứ ~v~ (~1 \le u,v \le K+M~).
Scoring
Với mỗi test, gọi ~B~ là tổng độ dài dây điện trong phương án thiết kế của Bob. Số điểm (trên thang điểm ~1~) cho phương án này là:
$$\begin{cases} 1, & \text{nếu } B \le A, \\ 0, & \text{nếu } B > 1.03 \times A, \\ 13 - 12^{\frac{B}{A}}, & \text{nếu } A < B \le 1.03 \times A. \end{cases}$$
| Subtask | Điểm | Giá trị ~K~ | Dãy ~\alpha~ | Giá trị ~A~ |
|---|---|---|---|---|
| 1 | ~12\%~ | ~3~ | ~(0, 90, 180)~ | ~273.2056~ |
| 2 | ~14\%~ | ~3~ | ~(0, 40, 150)~ | ~230.5843~ |
| 3 | ~14\%~ | ~4~ | ~(40, 140, 200, 340)~ | ~341.1483~ |
| 4 | ~14\%~ | ~5~ | ~(0, 72, 144, 216, 288)~ | ~457.4330~ |
| 5 | ~6\%~ | ~6~ | ~(0, 60, 120, 180, 240, 300)~ | ~500.0000~ |
| 6 | ~40\%~ | Không có ràng buộc nào thêm | ||
Sample Input 1
3
0 120 240
300.0000
Sample Output 1
1
0.0000 0.0000
1 4
2 4
3 4
Notes
Thêm một điểm trung gian có tọa độ ~(0,0)~. Điểm trung gian này nối với ~3~ trại với tổng độ dài là ~300.0000~ mét.
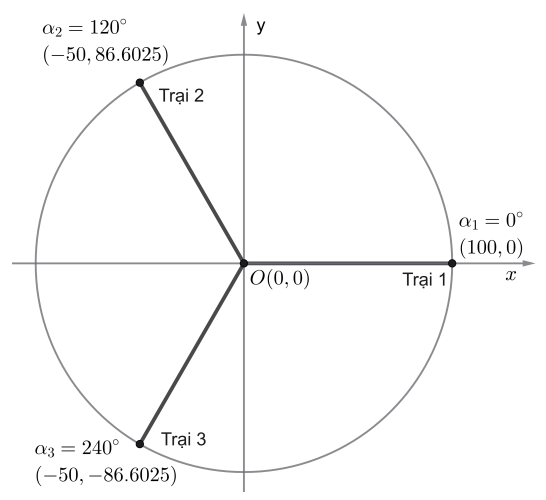
Lưu ý: Checker không chấp nhận in ra số thập phân dạng ~\texttt{-0.0000}~.

Bình luận