VOI 24 Bài 6 - Bài tập đêm giáng sinh
Xem dạng PDFCô Tuyết chuẩn bị một bài tập đặc biệt dành cho các bạn trong đội tuyển học sinh giỏi vào giáng sinh năm nay. Đó là môt bài tập về thứ tự từ điển với đề bài như sau.
Cho một dãy số khác rỗng ~C = [C_1, C_2, \ldots, C_M]~ thỏa mãn ~C_i \ne C_{i-1}, \forall i = 2, 3, \ldots, M~. Ta gọi một cách phân đoạn dãy là một cách chia dãy thành các đoạn con chứa các phần tử liên tiếp, mà mỗi phần tử đều thuộc đúng một đoạn con. Một cách phân đoạn dãy được coi là hợp lệ nếu mỗi đoạn con chỉ chứa các phần tử đôi một phân biệt.
Ví dụ, với ~M = 10~ và dãy ~C = [1,2,4,3,1,2,8,6,8]~, thì một cách phân đoạn dãy hợp lệ là chia dãy ~C~ thành ~4~ đoạn con lần lượt là ~[1,2,4,3],[2,1],[2,8],[6,8]~.

Một cách phân đoạn hợp lệ khác là chia dãy ~C~ thành ~5~ đoạn con lần lượt là ~[1,2,4],[3,2,1],[2,8],[6],[8]~.

Cả hai cách phân đoạn trên đều thỏa mãn mọi đoạn con chỉ chứa các phần tử đôi một phân biệt. Mặt khác, nếu ta chia dãy ~C~ thành ~4~ đoạn con lần lượt là ~[1,2,4,3],[2,1],[2],[8,6,8]~ thì sẽ không hợp lệ bởi có hai phần tử cùng bằng ~8~ trong đoạn con cuối cùng. Tương tự, nếu ta chia dãy ~C~ thành 5 đoạn con lần lượt là ~[1],[2,4,3,2,1,2],[8],[6],[8]~ thì cũng không hợp lệ bởi có ba phần tử cùng bằng ~2~ trong đoạn con thứ hai.
Mỗi dãy có thể có nhiều cách phân đoạn dãy hợp lệ. Mỗi cách phân đoạn dãy được mã hóa bằng một dãy mã hóa phân đoạn ~A = [A_1, A_2, \ldots, A_K]~, với ~K~ là số lượng đoạn con, và ~A_i~ là số lượng phần tử của đoạn con thứ ~i~. Chẳng hạn, với ~M=10~ và dãy ~C = [1,2,4,3,2,1,2,8,6,8]~, thì cách phân đoạn dãy trong hình đầu tiên sẽ được mã hóa bằng dãy ~A = [4,2,2,2]~.
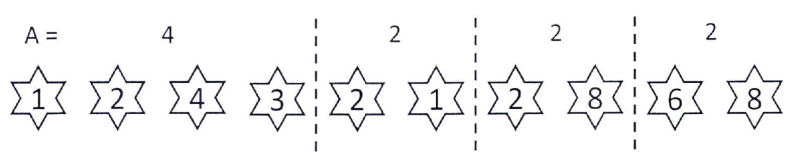
Tương tự, cách phân đoạn dãy trong hình thứ hai sẽ được mã hóa thành dãy ~A = [3,3,2,1,1]~

Cô Tuyết viết lên bảng một dãy số khác rỗng ~C = [C_1, C_2, \ldots, C_M]~ thỏa mãn ~C_i \ne C_i-1, \forall i = 2,3,\ldots,M~, rồi lại viết lên bảng thêm ~2~ số nguyên dương ~X~ và ~Y~. Sau đó cô gọi một bạn lên bảng để trả lời câu hỏi sau:
"Khi liệt kê tất cả các dãy mã hóa phân đoạn của dãy ~C~ rồi sắp xếp chúng theo thứ tự từ điển ngược thì dãy mã hóa phân đoạn thứ ~X~ và dãy mã hóa phân đoạn thứ ~Y~ có độ dài tiền tố chung dài nhất là bao nhiêu?"
Nhắc lại: Một dãy mã hóa phân đoạn ~U = [U_1, U_2, \ldots, U_K]~ gọi là đi trước dãy mã hóa phân đoạn ~V = [V_1, V_2, \ldots, V_H]~ theo thứ tự từ điển ngược nếu thỏa mãn một trong hai điều kiện sau:
~K > H~ và ~U_i = V_i, \ \forall i = 1,2,\ldots,H~;
Tồn tại ~1 \le T \le min(K,H)~ sao cho ~U_i = V_i, \ \forall i = 1,2,\ldots,T - 1~ và ~U_T > V_T~.
Dãy số ~U = [U_1, U_2, \ldots, U_K]~ được gọi là tiền tố độ dài ~K~ của dãy ~V = [V_1, V_2, \ldots, V_H]~ khi và chỉ khi ~K\le H~ và ~U_i = V_i, \forall i = 1,2,\ldots, K~. Lưu ý, dãy rỗng (ký hiệu là ~[]~) là tiền tố độ dài ~0~ của mọi dãy số.
Tiền tố chung dài nhất của hai dãy số ~Z_1~ và ~Z_2~ là dãy số có độ dài lớn nhất vừa là tiền tố của dãy ~Z_1~ vừa là tiền tố của dãy ~Z_2~.
Nhận thấy rằng nếu chỉ đặt ra câu hỏi cho một cặp số ~(X,Y)~ thì bài toán chưa đủ khó, cô Tuyết quyết định thềm vào một vài tham số mới. cô gọi ~Q~ bạn lần lượt lên bảng, bạn thứ ~i~ sẽ nhận được ~4~ số ~L_i, R_i, X_i, Y_i~ và có nhiệm vụ trả lời câu hỏi sau:
"Khi liệt kê tất cả các dãy mã hóa phân đoạn của dãy ~C' = [C_{L_i}, C_{L_i + 1}, \ldots, C_{R_i}]~ rồi sắp xếp chúng theo thứ tự từ điển ngược thì dãy mã hóa phân đoạn thứ ~X_i~ và dãy mã hóa phân đoạn thứ ~Y_i~ có độ dài tiền tố chung dài nhất là bao nhiêu?"
Yêu cầu: Hãy giúp các bạn trả lời ~Q~ câu hỏi của cô Tuyết.
Input
Vào từ file văn bản NOEL.INP:
Dòng đầu chứa hai số nguyên ~M~ và ~Q~ lần lượt là độ dài của dãy ~C~ và số lượng bạn được cô Tuyết gọi lên bảng ~(1 \le M,Q \le 2 \times 10^5)~
Dòng thứ hai chứa ~M~ số nguyên ~C_1, C_2, \ldots, C_M~ ~(1 \le C_i \le M, \forall i = 1,2, \ldots, M~; ~C_i \ne C_{i-1}~, ~\forall i = 2,3,\ldots,M)~.
Dòng thứ ~i~ trong số ~Q~ dòng tiếp theo biểu diễn một câu hỏi với bốn số nguyên ~L_i,R_i,X_i,Y_i~ ~(1 \le L_i \le R_i \le M; 1 \le X_i,Y_i \le 10^{17})~. Dữ liệu bảo đảm một số lượng dãy mã hóa phân đoạn của dãy ~C' = [C_{L_i}, C_{L_i + 1}, \ldots, C_{R_i}]~ không nhỏ hơn ~max(X_i,Y_i)~.
Các số trên dùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra file văn bản NOEL.OUT:
- Gồm ~Q~ dòng, trong đó dòng thứ ~i~ chứa một số nguyên là độ dài tiền tố chung dài nhất của hai dãy mã hóa phân đoạn của dãy ~C' = [C_{L_i}, C_{L_i + 1}, \ldots, C_{R_i}]~, với dãy mã hóa thứ nhất có thứ tự từ điển ngược bằng ~X_i~ và dãy mã hóa thứ hai có thứ tự từ điển ngược bằng ~Y_i~.
Scoring
Ràng buộc
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~17,5\%~ | ~M \le 12~ và ~Q \le 1024~. |
| 2 | ~20\%~ | ~X_i = Y_i = 1, \forall i = 1,2,\ldots, Q~. |
| 3 | ~22,5\%~ | ~L_i = 1; R_i = M~ và ~X_i, Y_i \le 10^5, \forall i = 1, 2, \ldots, Q~. |
| 4 | ~22,5\%~ | ~M \le 2000~ và ~Q \le 20000~ . |
| 5 | ~17,5\%~ | Không có ràng buộc gì thêm. |
Sample Input 1
10 2
1 2 4 3 2 1 2 8 6 8
2 5 6 7
4 10 7 6
Sample Output 1
2
0
Notes
Trong câu hỏi đầu tiên, dãy cần xét đến là ~C' = [2,4,3,2]~. Tất cả các dãy mã hóa phân đoạn sắp xếp theo thứ tự từ điển ngược lần lượt là ~[3,1]; [2,2]; [2,1,1]; [1,3]; [1,2,1]; [1,1,2]; [1,1,1,1]~. Hai dãy mã hóa phân đoạn có thứ tự từ điển ngược bằng ~6~ và bằng ~7~ tương ứng là ~Z_1 = [1,1,2]~ và ~Z_2 = [1,1,1,1]~. Độ dài tiền tố chung dài nhất của hai dãy ~Z_1~ và ~Z_2~ là ~2~.
Trong câu hỏi thứ hai, dãy cần xét đến là ~C' = [3,2,1,2,8,6,8]~. Hai dãy mã hóa phân đoạn có thứ tự từ điển ngược bằng ~7~ và bằng ~6~ tương ứng là ~Z_1 = [2,4,1]~ và ~Z_2 = [3,1,1,1,1]~. Độ dài tiền tố chung dài nhất của hai dãy ~Z_1~ và ~Z_2~ là ~0~.

Bình luận
orz
.
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.