Lưu ý: Đọc input, output từ stdin/stdout

Một thành phố có ~N~ địa điểm được đánh số từ ~1~ đến ~N~, có ~M~ đoạn đường hai chiều, đoạn đường thứ ~i~ ~(1 \leq i \leq M)~ nối hai địa điểm ~u_i~, ~v_i~ ~(1 \leq u_i, v_i \leq N)~ với độ dài ~w_i~.

Nhóm bạn thân của Nam có ~K~ người đều sống trong thành phố, Nam được đánh chỉ số ~1~ và các bạn của Nam được đánh chỉ số lần lượt từ ~2~ đến ~K~. Ngày chủ nhật tới được nghỉ học, mỗi bạn trong nhóm sẽ chạy bộ đến công viên ưa thích của mỗi người để tập thể dục. Người thứ ~i~ ~(1 \leq i \leq K)~ có nhà nằm ở địa điểm ~a_i~ ~(1 \leq a_i \leq N)~ và chủ nhật sẽ tập thể dục ở công viên ưa thích nằm ở địa điểm ~b_i~ ~(1 \leq b_i \leq N)~. Để tiết kiệm thời gian, mỗi người sẽ xuất phát từ nhà đi tới công viên theo một đường đi có độ dài ngắn nhất.

Một đường đi gồm ~t~ địa điểm xuất phát từ địa điểm ~u~ và kết thúc tại địa điểm ~v~ là một chuỗi liên tiếp các địa điểm:

~u=c_1, c_2, ..., c_{t-1}, c_t= v~,

sao cho có đoạn đường nối trực tiếp giữa 2 địa điểm liên tiếp ~c_j~ và ~c_{j + 1}~ ~(1 \leq j < t)~ trong chuỗi. Độ dài của một đường đi là tổng độ dài của các đoạn đường nối trực tiếp 2 địa điểm liên tiếp trên đường đi đó.

Để việc tập thể dục trở nên vui vẻ hơn, Nam mong muốn có thể được đi chung với các bạn thân của mình trên đường đi tập thể dục. Nam được gọi là đi chung với một người bạn trên đoạn đường nối trực tiếp hai địa điểm ~u~ và ~v~ khi và chỉ khi đoạn đường này đều nằm trên đường đi tập thể dục của hai người và cả hai người đều đi đến địa điểm ~u~ tại cùng một thời điểm trước khi cùng nhau đi đến địa điểm ~v~. Gọi ~S~ là tổng độ dài của các đoạn đường mà Nam đi chung với ít nhất một người bạn thân của mình. Nam muốn giá trị của ~S~ là càng lớn càng tốt.

Chủ nhật, theo dự định, mỗi người đều sẽ xuất phát đi tập thể dục vào lúc ~7~ giờ sáng. Để có thể đạt được ~S~ là lớn nhất, Nam cố gắng thuyết phục mỗi người bạn thân của mình đi theo một đường đi ngắn nhất và xuất phát tại một thời điểm nào đó theo kế hoạch của Nam. Do đi theo đường đi có độ dài ngắn nhất nào cũng không làm thay đổi khoảng thời gian di chuyển trên đường nên tất cả đều đồng ý đi theo các lộ trình đường đi ngắn nhất mà Nam đề xuất. Tuy nhiên, việc thay đổi giờ xuất phát, trước hoặc sau ~7h~ sáng, có thể làm ảnh hưởng tới các kế hoạch cá nhân khác nên Nam chỉ thuyết phục được việc thay đổi thời gian xuất phát đối với những ai dễ tính mà thôi. Do đã quen với việc thức dậy sớm và xuất phát lúc ~7~ giờ sáng, Nam không thay đổi thời điểm xuất phát của mình.

Yêu cầu: Biết rằng để đi một đơn vị khoảng cách mất một đơn vị thời gian, biết danh sách những bạn dễ tính, hãy giúp Nam lên kế hoạch để đạt được ~S~ lớn nhất.

Input

• Dòng đầu tiên chứa ba số nguyên ~N~, ~M~ và ~K~ ~(1 \leq N \leq 10^ 5, 1 \leq M \leq 10^ 5,, 2 \leq K \leq 10)~;
• Dòng thứ ~i~ trong số ~M~ dòng tiếp theo chứa ba số nguyên ~u_i~, ~v_i~, ~w_i~ ~(1 \leq u_i, v_i \leq N, u_i \neq v_i, 1 \leq w_i \leq 10^9)~ mô tả đoạn đường hai chiều nối hai địa điểm ~u_i~ và ~v_i~ với độ dài ~w_i~. Dữ liệu đảm bảo luôn tồn tại đường đi giữa hai địa điểm bất kì và không có hai đoạn đường nào nối trực tiếp cùng một cặp địa điểm;
• Dòng tiếp theo chứa hai số nguyên ~a_1~ và ~b_1~ tương ứng là địa điểm xuất phát và địa điểm kết thúc đường đi tập của Nam;
• Dòng thứ ~i~ trong số ~K-1~ dòng tiếp theo, ~1 \le i \leq K-1~, chứa ba số nguyên ~p_{i+1}~, ~a_{i+1}~, ~b_{i+1}~ tương ứng là độ khó/dễ tính, địa điểm xuất phát và địa điểm kết thúc đường đi tập của người bạn có chỉ số ~i+1~, trong đó ~p_{i+1}~ bằng ~0~ nghĩa là khó tính và bằng ~1~ nếu dễ tính.

Các số trên cùng một dòng cách nhau bởi dấu cách.

Output

In ra 1 số nguyên duy nhất là giá trị lớn nhất của ~S~.

Scoring

• Có ~20\%~ số lượng test ứng với ~20\%~ số điểm của bài thỏa mãn điều kiện: ~K=2~, ~a_1=a_2~;
• ~20\%~ số lượng test khác ứng với ~20\%~ số điểm của bài thỏa mãn điều kiện: ~N \leq 100~, ~K=2~;
• ~30\%~ số lượng test khác ứng với ~30\%~ số điểm của bài thỏa mãn điều kiện: ~K=2~;
• ~20\%~ số lượng test khác ứng với ~20\%~ số điểm của bài thỏa mãn điều kiện: toàn bộ ~K-1~ người bạn là khó tính;
• ~10\%~ số lượng test còn lại ứng với ~10\%~ số điểm của bài thỏa mãn điều kiện: số người bạn dễ tính không quá ~5~.

Sample Input

7 8 4 
2 1 2
2 4 2
4 3 2
4 5 1
1 5 3
1 7 3
5 6 2
7 6 8
1 4
0 3 2
1 7 6
0 1 2 

Sample Output

3

Giải thích

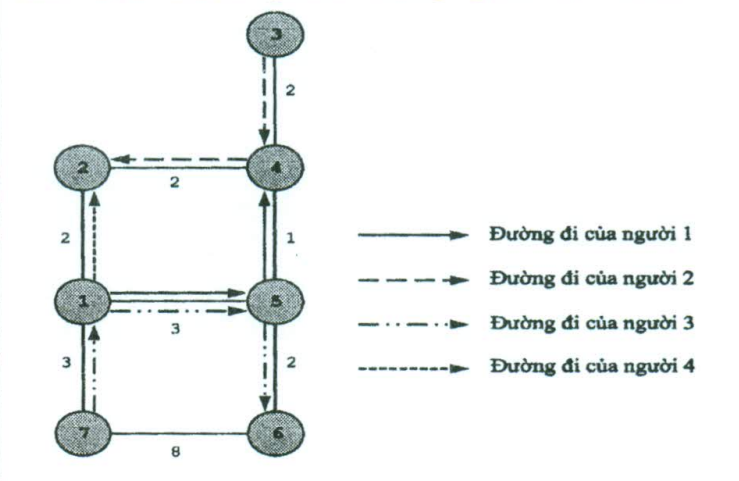
Người thứ ~3~ xuất phát trước giờ dự kiến ~3~ đơn vị thời gian. Những người còn lại xuất phát đúng giờ dự kiến.