Pira là một thành phố nổi tiếng với hệ thống tàu điện ngầm lâu đời và phức tạp. Thành phố có ~n~ ga tàu, được đánh số từ ~1~ đến ~n~ và ~m~ tuyến đường có số hiệu từ ~1~ đến ~m~. Tuyến đường có số hiệu ~k~ được biểu diễn bởi cặp có thứ tự gồm hai chỉ số của hai nhà ga ~(u_k, v_k)~ cho biết tuyến đường này cho phép đi từ ga ~u_k~ đến ga ~v_k~. Khi đó ta nói tuyến đường số hiệu ~k~ là đi khỏi ga ~u_k~ và đi đến ga ~v_k~. Thời gian cần thiết để mỗi chuyến tàu đi theo tuyến đường số hiệu ~k~ từ ga ~u_k~ đến ga ~v_k~ là ~t_k~ đơn vị thời gian.

Mỗi ga có các bến tàu đến tương ứng với mỗi tuyến đường đi đến nó và các bến tàu đi tương ứng với mỗi tuyến đường đi khỏi nó. Khi xây dựng hệ thống này, lãnh đạo thành phố đã nhờ các nhà khoa học tính toán và sắp xếp các vị trí đặt các bến tàu đến và các bến tàu đi trong mỗi ga sao cho hành khách dễ dàng di chuyển và tính được thời gian di chuyển theo cách lựa chọn của mình. Các nhà khoa học đã sắp xếp vị trí các bến tàu đến và đi ở mỗi ga sao cho thời gian di chuyển từ bến tàu đến của tuyến đường số hiệu ~i~ đến bến tàu đi của tuyến đường số hiệu ~j~ được tính bởi hàm ~F(i, j) = i \times \delta + j~, trong đó ~\delta~ là một thông số mà các nhà khoa học đư vào để hàm ~F(i, j)~ có thể thay đổi linh hoạt tuỳ thời điểm. Nói một cách đơn giản, nếu trên đường di chuyển hành khách theo tuyến đường ~i~ đi đến một ga nào đó và theo tuyến đường ~j~ đi khỏi ga này thì sẽ mất ~F(i, j)~ đơn vị thời gian để thực hiện việc chuyển tuyến đường. Do đó ta gọi ~F(i, j)~ là hàm chi phí thời gian chuyển tuyến để chuyển từ tuyến đường ~i~ sang tuyến đường ~j~.

Dựa vào thông tin về thời gian di chuyển trên các tuyến đường và hàm chi phí thời gian chuyển tuyến ~F(i, j)~, hành khách có thể tính được thời gian di chuyển từ một ga đến bất kỳ ga nào còn lại trong hệ thống là bằng tổng thời gian di chuyển trên các tuyến đường giữa các ga và thời gian chuyển tuyến ở mỗi ga trung gian.

Yêu cầu: Cho biết vị trí hai ga ~u~ và ~v~ trong hệ thống, hãy tính thời gian ít nhất để di chuyển từ ga ~u~ đến ga ~v~.

Input

• Dòng thứ nhất ghi các số nguyên dương ~n~, ~m~, ~u~, ~v~ và số nguyên không âm ~\delta~, trong đó ~\delta~ ~(\delta \le 100)~ là thông số xác định hàm chi phí chuyển tuyến;
• Dòng thứ ~k~ trong số ~m~ dòng tiếp theo chứa ba số nguyên dương ~u_k~, ~v_k~ và ~t_k~ mô tả thông tin về tuyến đường số hiệu ~k~ cho biết tuyến đường này cho phép di chuyển từ ga ~u_k~ đến ga ~v_k~ và ~t_k~ ~(t_k \le 10^9)~ là thời gian di chuyển qua nó, ~k = 1, 2, \ldots, m~.

Dữ liệu đảm bảo có không quá một tuyến đường đi từ ga ~p~ đến ga ~q~ với mọi ~p~ và ~q~ và không có tuyến đường nào nối một ga với chính nó. Các số trên cùng dòng được ghi cách nhau bởi dấu cách.

Output

Ghi ra một số nguyên là thời gian di chuyển tìm được. Nếu không có cách di chuyển thì ghi ra ~-1~.

Giới hạn

• Có ~40\%~ số lượng test thoả mãn điều kiện: ~n \le 10^3, m \le 10^5, \delta = 0~;
• Có thêm ~30\%~ số lượng test thoả mãn điều kiện: ~n \le 10^5, m \le 10^5, \delta = 0~;
• ~30\%~ số lượng test còn lại thoả mãn điều kiện: ~n \le 10\,000, m \le 50\,000, \delta \ge 1~.

Sample Input

5 8 1 5 1
1 2 12
1 3 13
1 4 14
4 2 14
2 3 12
2 5 12
4 5 15
3 5 16

Sample Output

31

Note

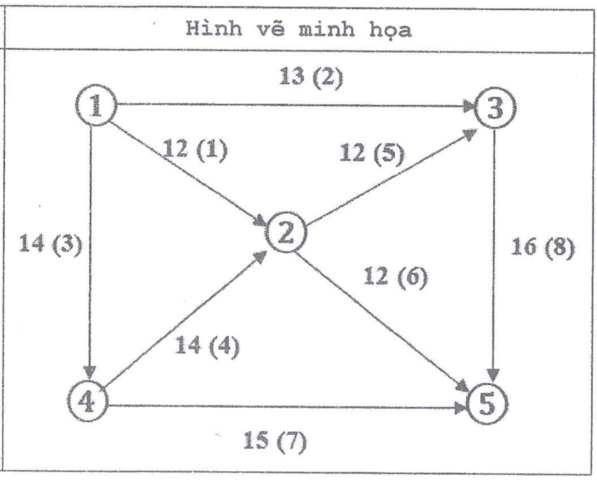
Giải thích:

• Cặp số ~a~ ~(b)~  viết bên mỗi cung trên hình vẽ minh hoạ là thời gian di chuyển và số hiệu của tuyến đường.
• Hành khách đi từ ga ~1~ đến ga ~2~ mất ~12~ đơn vị thời gian, di chuyển từ bến tàu đến của tuyến đường số hiệu ~1~ đến bến tàu đi của tuyến đường số hiệu ~6~ ở ga ~2~ mất thời gian chuyển tuyến ~(1 \times 1 + 6) = 7~ đơn vị thời gian và di chuyển từ ga ~2~ đến ga ~5~ mất ~12~ đơn vị thời gian. Tổng cộng thời gian di chuyển là: ~12 + 7 + 12 = 31~.
• Chú ý: Vẫn với ví dụ trên, nhưng thay ~\delta = 0~ thì cách đi với thời gian ít nhất từ ga ~1~ đến ga ~5~ là: ~12 + 6 + 12 = 30~.