VO 13 Bài 2 - Xương rồng
Xem dạng PDFCây xương rồng vẫn mãi xanh và căng tràn nhựa sống cho dù quanh năm suốt tháng không ai ngó ngàng chăm sóc. Nhưng bất hạnh thay, không ai có thể chạm đến được những gì tốt đẹp nhất của cây bởi một lời nguyền độc ác: xương rồng có gai. Chính vì vậy, xương rồng phải sống một cuộc đời cô đơn bất tận...
Những người yêu Tin học của vương quốc cô đơn nhìn thấy hình ảnh của chính mình trong cây xương rồng. Vì vậy, họ luôn cố gắng đưa hình ảnh xương rồng vào những công trình nghiên cứu. Đồ thị cũng không phải là ngoại lệ. Đồ thị xương rồng khá phổ biến ở vương quốc cô đơn: một đồ thị vô hướng có trọng số và có một tính chất đặc biệt là mỗi cạnh thuộc vào nhiều nhất là một chu trình.
Lưu ý rằng, vì ta đang ở vương quốc cô đơn nên định nghĩa chu trình cũng khác biệt với thế giới bên ngoài. Thuật ngữ "chu trình" chỉ một đường đi trên đồ thị có đỉnh đầu và cuối trùng nhau và các đỉnh khác trên đường đi được đi qua tối đa một lần.
Hiện tại, những con người cô đơn và đam mê Tin học nói trên đang rất có hứng thú về bài toán đường đi ngắn nhất trên đồ thị. Tuy nhiên, cũng vì nỗi ảm ảnh về sự cô đơn nên quá trình nghiên cứu của họ đang bị đánh lạc sang một hướng hẹp:
- Người cô đơn vô cùng căm thù số chẵn (thay vì nói "~2~ bàn tay có ~10~ ngón" thì họ sẽ nói "~1~ bàn tay có ~5~ ngón"). Vì vậy, những đường đi mà họ quan tâm phải đi qua một số lẻ đỉnh.
- Ngoài ra, những đường đi nói trên cũng phải là đường đi đơn, tức là mỗi đỉnh trên đường đi chỉ được đi qua tối đa một lần.
Càng ngày càng có nhiều người muốn làm cư dân của vương quốc cô đơn. Nhưng muốn trở thành một người cô đơn thực thụ thì phải thể hiện được hiểu biết về đồ thị và tình yêu đối với xương rồng bằng cách trả lời được câu hỏi sau:
Bạn được cho một đồ thị xương rồng, hãy tìm đường đi đơn đi qua một số lẻ đỉnh ngắn nhất (tổng trọng số các cạnh nhỏ nhất) giữa hai đỉnh cho trước của đồ thị.
Bạn cảm thấy xung quanh mình thật trống trải và muốn gia nhập vương quốc cô đơn? Hãy trả lời câu hỏi trên.
Input
- Dòng thứ nhất chứa bốn số nguyên dương ~N~, ~M~, ~S~, ~T~, tương ứng với số đỉnh, số cạnh, đỉnh bắt đầu và đỉnh kết thúc trong đường đi cần tìm.
- ~M~ dòng tiếp theo: mỗi dòng chứ ba số nguyên dương ~u~, ~v~, ~c~, thể hiện một cạnh ~(u~, ~v)~ với trọng số ~c~.
Output
- Một số nguyên dương duy nhất là độ dài của đường đi tìm được. Nếu không tồn tại đường đi thỏa yêu cầu, in ra ~-1~.
Giới hạn
- ~1 \leq N~, ~M \leq 10^{5}~. ~1 \leq S~, ~T \leq N~, ~S~ khác ~T~.
- Trong ~30\%~ số test có ~1 \leq N~, ~M \leq 20~.
- Trong ~30\%~ số test tiếp theo, đồ thị không có chu trình lẻ.
- Mỗi cạnh có trọng số không quá ~10^{4}~.
- Đồ thị đã cho đảm bảo là một đồ thị xương rồng. Ngoài ra, đồ thị không có cạnh nối một đỉnh với chính nó và giữa một cặp đỉnh chỉ có tối đa một cạnh nối.
Sample Input
10 12 5 10
1 2 2
1 3 1
3 4 1
4 5 2
3 5 3
2 6 4
3 6 8
6 7 1
6 8 3
8 9 2
8 10 2
9 10 1
Sample Output
15
Note
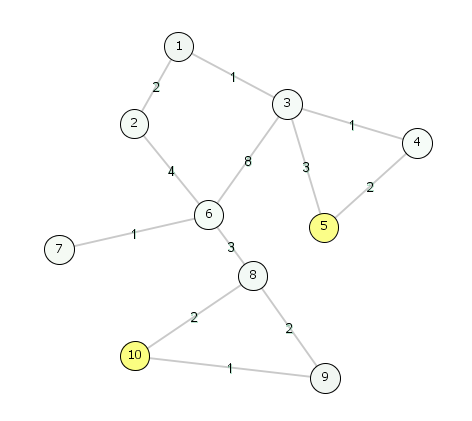
Đường đi: ~5 - 3 - 1 - 2 - 6 - 8 - 10~
Bình luận