VNOJ Round 01 - TREE PATH
Xem dạng PDFNauw có một cây gồm ~n~ đỉnh và ~n-1~ cạnh. Độ đẹp ~h(u, v)~ của một cặp điểm ~u, v~ là số lượng các trọng số cạnh xuất hiện nhiều hơn ~1~ lần trong đường đi từ ~u \rightarrow v~.
Cụ thể, ta gọi các trọng số cạnh trên đường đi từ ~u \rightarrow v~ là ~w_1, w_2, w_3, ..., w_k~ thì ~h(u, v)= \sum_{i=1}^{k} (p(w_i)>1)~, với ~p(w_i)~ là số lần xuất hiện của ~w_i~ trong mảng ~w~.
Độ đẹp của cả cây sẽ bằng tổng của tất cả các ~h(u, v)~ với mọi ~u, v~ (~1 \le u < v \le n~). Hãy tính độ đẹp của cây.
Input
Dòng đầu chứa số nguyên dương ~n~ (~3\le n \le 10^5~) thể hiện số lượng đỉnh.
~n-1~ dòng tiếp theo mỗi dòng chứa ba số nguyên dương ~u, v, w~ (~1\le u \neq v \le n, w \le n~) thể hiện một cạnh của cây.
Output
- In ra một số nguyên dương duy nhất là kết quả của bài.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20~ | ~3\le n \le 300~ |
| 2 | ~30~ | Cạnh thứ ~i~ nối đỉnh ~i~ và đỉnh ~i+1~. |
| 3 | ~50~ | Không có ràng buộc gì thêm |
Sample Input 1
3
1 2 3
3 2 3
Sample Output 1
2
Sample Input 2
4
1 4 2
4 2 2
3 4 1
Sample Output 2
2
Notes
Ở test ví dụ thứ ~1~:
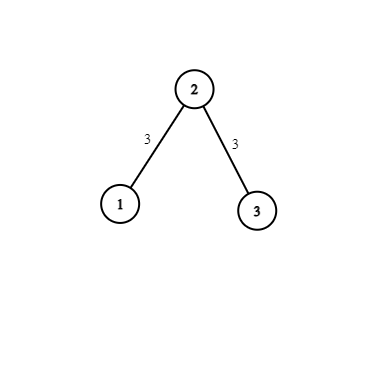
Chỉ có ~h(1, 3)=2~, còn lại tất cả các cặp khác đều là ~0~.
~\Rightarrow~ Đáp án là ~2~.
Ở test ví dụ thứ ~2~:
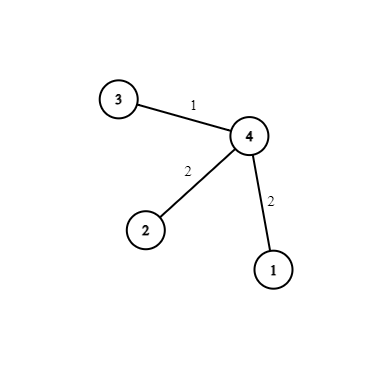
Chỉ có ~h(1, 2)=2~, còn lại tất cả các cặp khác đều là ~0~.
~\Rightarrow~ Đáp án là ~2~.

Bình luận