Subtask 1: ~n, m, h, w, a_i, b_i \leq 50~

Với giới hạn nhỏ, ta có thể giải bằng quy hoạch động cơ bản. Giả sử kích thước tối ưu cuối cùng là ~(x, y)~. Vì ~x~ và ~y~ đều dương nên hiển nhiên với ~x~ cố định thì việc tìm ~y~ sao cho ~x^2 + y^2~ lớn nhất tương đương với tìm ~y~ lớn nhất. Vậy ta quy hoạch động ~dp(r, c, x)~ là chiều rộng lớn nhất có thể khi MofK tới giao lộ ~(r, c)~ và chiều cao hiện tại của TV là ~x~. Công thức quy hoạch động đơn giản là:

• ~dp(1, 1, h + a_1) = w + b_1~
• ~dp(r, c, x) = \max(dp(r-1, c, x - a_r),\, dp(r, c-1, x - a_r)) + b_c~

Đáp số là ~\max\limits_{x} \, (x^2 + dp(n, m, x)^2)~.

Số trạng thái của hàm QHĐ trên là ~O(n\times m\times (h + n\times \max a_i))~ và chuyển trạng thái trong ~O(1)~.

Subtask 2: ~h, w, a_i, b_i \leq 1\,000~

Ta thử giải bài toán đơn giản hơn: thay vì tối ưu ~x^2 + y^2~, ta sẽ tối ưu ~x + y~. Đây là một bài toán cổ điển đã từng xuất hiện ở nhiều nơi, trong đó có subtask 3 của bài G vòng Chung kết VNOI Cup 2023. Để bài viết này được ngắn gọn, các bạn có thể tham khảo chứng minh tại đây. Tóm tắt cách giải bài toán con này như sau:

• Chia dãy ~a~ thành các đoạn con có trung bình cộng giảm dần, nghĩa là nếu chia ~a~ thành các đoạn ~(sum_i, cnt_i)~ với ~sum_i~ và ~cnt_i~ lần lượt là tổng các phần tử và số phần tử của đoạn thứ ~i~ thì ~\frac{sum_i}{cnt_i} > \frac{sum_{i+1}}{cnt_{i+1}}~. Làm tương tự với dãy ~b~.
• Sắp xếp lại các đoạn của hai dãy theo thứ tự trung bình cộng giảm dần.
• Xuất phát từ ~(1, 1)~, xét lần lượt các đoạn theo thứ tự đã sắp xếp ở trên. Giả sử vị trí hiện tại là ~(r, c)~ và đoạn tiếp theo được xét là ~(sum_i, cnt_i)~ thuộc dãy ~a~, ta đi tới ~(r + cnt_i, c)~ và cập nhật kết quả. Ngược lại nếu đoạn đó thuộc dãy ~b~ thì ta đi tới ~(r, c + cnt_i)~ và cập nhật kết quả.

Vậy bài toán con được giải với độ phức tạp ~O(n+m)~. Ngoài ra, nếu ta cần tối ưu ~px + qy~ (với ~p, q \geq 0~) thay vì ~x + y~, ta chỉ cần biến đổi các đoạn ~(sum_i, cnt_i)~ của dãy ~a~ thành ~(p\times sum_i, cnt_i)~, tương tự các đoạn của dãy ~b~ thành ~(q\times sum_i, cnt_i)~ rồi giải như trên.

Quay trở lại với bài toán gốc. Ta biểu diễn mỗi cách đi của MofK bằng một điểm ~(x, y)~ trên mặt phẳng tọa độ, trong đó ~x~ và ~y~ là chiều cao và chiều rộng của TV sau khi thực hiện cách đi đó. Ta cần tìm điểm ~(x, y)~ có ~x^2 + y^2~ lớn nhất. Ta chứng minh rằng điểm tối ưu phải nằm trên bao lồi của tập tất cả các điểm được xét. Thật vậy, theo định nghĩa, tất cả các điểm còn lại phải nằm trong hình tròn ~C~ có tâm ~(0, 0)~ và bán kính ~\sqrt{x^2+y^2}~ (xem hình dưới). Do đó, bao lồi của các điểm còn lại nằm hoàn toàn trong hình tròn ~C~ và không thể chứa ~(x, y)~, điều phải chứng minh.

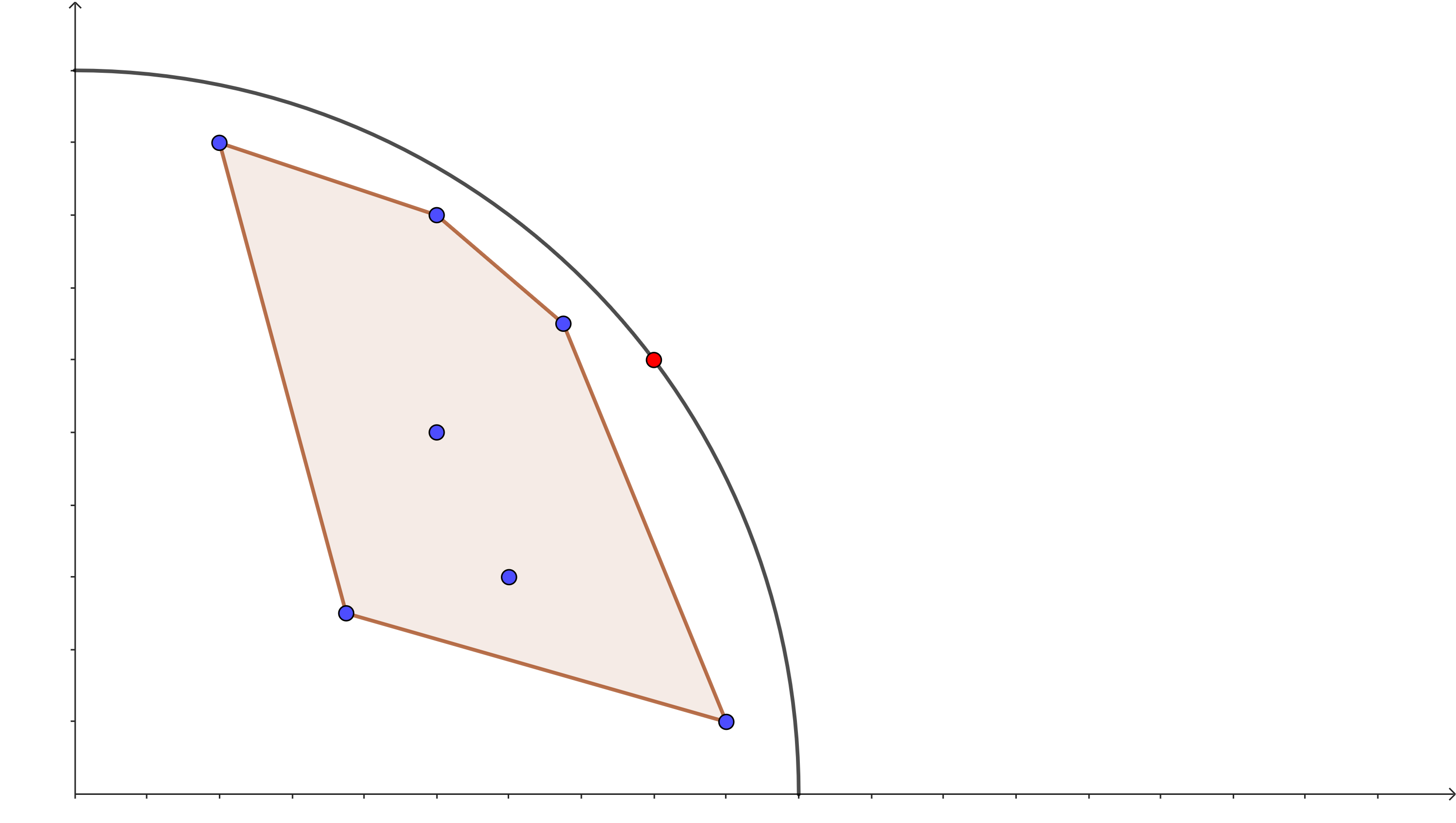
Từ nhận xét trên, ta có cách giải sau: tìm mọi điểm nằm trên bao lồi, sau đó kiểm tra tất cả các điểm đó để tìm đáp án. Ta tìm bao lồi tương tự như bài cổ điển BOI11 Time is Money:

• Tìm điểm có ~x~ lớn nhất bằng cách giải bài toán con với ~p = 1~, ~q = 0~. Tương tự tìm điểm có ~y~ lớn nhất bằng cách chọn ~p = 0~, ~q = 1~.
• Xét hai điểm ~(x, y)~ và ~(u, v)~ liên tiếp nhau trên bao lồi hiện tại, ta tìm một điểm trên bao lồi nằm giữa hai điểm này (nếu có) bằng cách giải bài toán con với ~p = x-u~, ~q = v-y~. Nếu điểm ~(s, t)~ tìm được thẳng hàng với ~(x, y)~ và ~(u, v)~ thì ta bỏ qua, ngược lại ta đệ quy xuống hai cặp điểm ~(x, y), (s, t)~ và ~(s, t), (u, v)~.

Độ phức tạp của thuật toán trên là ~O(H\times (n+m))~, trong đó ~H~ là số điểm nằm trên bao lồi. Theo giới hạn subtask, tọa độ các điểm không vượt quá ~1000(n+m) \leq 2\times 10^6~, do đó số điểm tối đa trên bao lồi rơi vào khoảng ~10^4~ (xem thảo luận và chứng minh tại đây).

Subtask 3: không có giới hạn gì thêm

Ta cần cải tiến lời giải của subtask 2. Để ý rằng tối ưu ~px + qy~ tương đương với tối ưu ~\alpha x + y~ với ~\alpha = \frac{p}{q}~, và khi ~\alpha~ thay đổi thì thứ tự của các đoạn con của dãy ~a~ không thay đổi, tương tự với dãy ~b~; chỉ có thứ tự giữa đoạn ~(sum_i, cnt_i)~ thuộc dãy ~a~ và đoạn ~(sum_j, cnt_j)~ thuộc dãy ~b~ bị hoán đổi khi ~\alpha = \frac{sum_j cnt_i}{sum_i cnt_j}~. Vậy ta có thể thực hiện thuật toán "sweep line" như sau:

• Giải bài toán con với ~p = 1, q = \infty~ (có thể dùng một giá trị lớn thay thế ~\infty~, chẳng hạn ~10^{12}~). Lưu lại thứ tự hiện tại của các đoạn con được sắp xếp theo trung bình cộng giảm dần.
• Với mỗi cặp đoạn ~(sum_i, cnt_i)~ thuộc dãy ~a~ và ~(sum_j, cnt_j)~ thuộc dãy ~b~, hoán đổi thứ tự của chúng tại ~\alpha = \frac{sum_j cnt_i}{sum_i cnt_j}~.
• Sắp xếp các ~\alpha~ theo thứ tự tăng dần, hoán đổi vị trí của cặp đoạn tương ứng và cập nhật lại kết quả. Việc này có thể làm trong ~O(1)~.

Chi tiết cài đặt xin nhường lại bạn đọc.

Do có tối đa ~nm~ giá trị ~\alpha~ cần xét, độ phức tạp của thuật toán trên là ~O(nm \log(nm))~ (từ bước sort các ~\alpha~).

Nộp một lời giải chính thức trước khi tự giải là một hành động có thể bị ban.
Nộp một lời giải chính thức trước khi tự giải là một hành động có thể bị ban.
Nộp một lời giải chính thức trước khi tự giải là một hành động có thể bị ban. (cái gì quan trọng nhắc lại 3 lần)