Cắt bảng
Xem dạng PDFSau sự cố tại bài thi sát hạch pháp sư hạng nhất, Hiệp Hội Pháp Sư Châu Lục đã quyết định sẽ vĩnh viễn bỏ bài thi này và thay thế bằng một bài thi tương tự, vừa đòi hỏi khả năng sử dụng ma pháp, vừa yêu cầu tư duy toán học đến từ thí sinh. Bài thi được đề ra như sau:
Sẽ có hai bảng số ~a~ và ~b~, mỗi bảng gồm ~n~ dòng và ~m~ cột được vẽ ra bằng ma pháp. Các dòng được đánh số từ ~1~ đến ~n~ từ trên xuống dưới, các cột được đánh số từ ~1~ đến ~m~ từ trái qua phải.
Trong quá trình thực hiện bài thi, thí sinh có thể dùng ma pháp để thực hiện các phép biến đổi bảng số ~a~ thuộc một trong hai loại sau (với số lần và trình tự tùy ý):
Đảo dọc: Chọn đường cắt giữa hai cột ~y~ và ~y+1~ (~1 \le y < m~). Chia bảng thành hai nửa trái–phải, hoán đổi chúng rồi ghép lại. Khi đó cột ~j \le y~ chuyển thành ~j + (m - y)~, còn cột ~j > y~ chuyển thành ~j - y~.
Đảo ngang: Chọn đường cắt giữa hai dòng ~x~ và ~x+1~ (~1 \le x < n~). Chia bảng thành hai nửa trên–dưới, hoán đổi chúng rồi ghép lại. Khi đó dòng ~i \le x~ chuyển thành ~i + (n - x)~, còn dòng ~i > x~ chuyển thành ~i - x~.
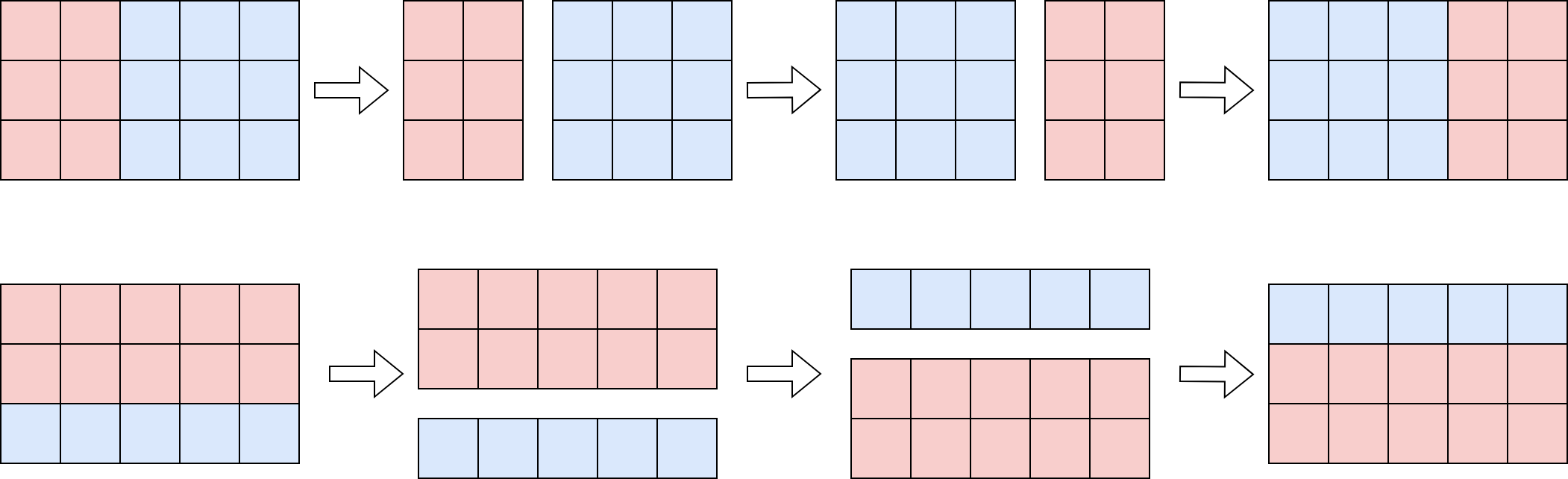
Hình vẽ minh họa hai loại phép biến đổi bảng
Để hoàn thành bài thi, thí sinh cần biến đổi bảng số ~a~ thành bảng số ~b~ chỉ bằng hai loại phép biến đổi trên.
Hãy giúp thí sinh kiểm tra xem có tồn tại cách để hoàn thành bài thi hay không.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 50~). Mô tả của mỗi test case như sau.
Dòng đầu tiên gồm hai số nguyên ~n~ và ~m~ (~1 \le n, m \le 50~) – kích thước của hai bảng số.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo gồm ~m~ số nguyên ~a_{i,1}, a_{i,2}, \ldots, a_{i,m}~ (~1 \le a_{i,j} \le 10^4~) – các số trên dòng ~i~ của bảng ~a~.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo gồm ~m~ số nguyên ~b_{i,1}, b_{i,2}, \ldots, b_{i,m}~ (~1 \le b_{i,j} \le 10^4~) – các số trên dòng ~i~ của bảng ~b~.
Dữ liệu vào đảm bảo:
Tổng giá trị ~n~ của các test case không vượt quá ~50~.
Tổng giá trị ~m~ của các test case không vượt quá ~50~.
Output
Với mỗi bộ dữ liệu vào, nếu tồn tại cách biến đổi bảng thỏa yêu cầu đề bài, in ra YES. Ngược lại, in ra NO.
Scoring
Tổng điểm cho bài này là ~500~.
Sample Input 1
2
3 4
1 2 5 2
5 7 4 6
2 3 1 3
3 2 3 1
2 1 2 5
6 5 7 4
2 2
1 1
1 1
1 1
2 2
Sample Output 1
YES
NO
Notes
Ở ví dụ đầu tiên, tồn tại cách biến đổi bảng như sau:
Đảo dọc với đường cắt giữa cột ~1~ và cột ~2~
Đảo ngang với đường cắt giữa dòng ~2~ và dòng ~3~
Đảo dọc với đường cắt giữa cột ~2~ và cột ~3~
Hình vẽ minh họa ví dụ 1
Ở ví dụ thứ hai, dù thực hiện phép biến đổi nào thì bảng ~a~ vẫn sẽ không thay đổi, do đó không tồn tại cách biến đổi bảng ~a~ thành bảng ~b~.
Bình luận
Tôi tin chắc là chỉ có Frieren mới giải được bài này :))) Còn người ra đề chắc là Serie á.
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.