Thần rừng tập sự
Xem dạng PDFTo read the problem statement in English, choose the language using the flag on the navigation bar.
Mỗi vị thần rừng đều quản lý một khu rừng. Mỗi khu rừng có ~n~ vị trí đánh số ~1~ đến ~n~, và mỗi vị trí có tối đa một cây.
Ai cũng biết một vị thần rừng có cấp bậc ~k~ có thể thực hiện hai câu thần chú sau để biến đổi khu rừng của mình:
Nếu như trong khu rừng không có cây nào ở vị trí ~p~ (~k < p \le n~), nhưng có các cây ở vị trí ~p - 1, p - 2, \ldots, p - k~, vị thần rừng có thể phù phép để gộp ~k~ cây này lại và tạo ra cây một cây mới tại vị trí ~p~. Sau khi phù phép, các cây ở vị trí ~p - 1, p - 2, \ldots, p - k~ sẽ biến mất, và một cây mới tại vị trí ~p~ sẽ mọc lên.
Nếu như trong khu rừng đang có một cây tại vị trí là ~p~ (~k < p \le n~), và không có cây tại các vị trí ~p - 1, p - 2, \ldots, p - k~, vị thần rừng có thể phù phép để biến cây này thành ~k~ cây tại các vị trí nói trên. Sau khi phù phép, cây tại vị trí ~p~ sẽ biến mất, và tại các vị trí ~p - 1, p - 2, \ldots, p - k~ sẽ có các cây mới mọc lên.
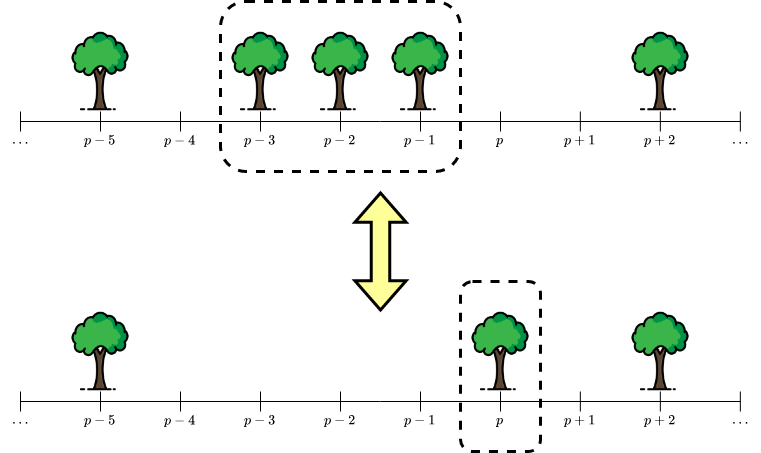
Minh họa cho hai câu thần chú của vị thần rừng với cấp bậc ~k = 3~.
Hiện tại có hai vị thần rừng tập sự có cấp bậc ~k~ là Quang và Tùng.
Quang quản lý khu rừng Q, còn Tùng quản lý khu rừng T. Quang là một
vị thần rừng chăm chỉ, ngày nào cũng luyện tập hai câu thần chú một cách
nhuần nhuyễn để biến đổi khu rừng của mình. Nhưng Tùng thì ngược lại.
Như một chú mèo, Tùng rất thích leo cây trong rừng của mình, nhưng sau
khi leo cây xong thì hay quên đường xuống. Vì thường xuyên bị mắc kẹt
trên cây, nên Tùng cũng không hay luyện tập biến biến đổi khu rừng của
mình.
Sau một thời gian, nhờ chăm chỉ luyện tập, Quang đã làm khu rừng Q của
mình trở nên đẹp đẽ, bạt ngàn. Còn khu rừng T của Tùng do không được
chăm sóc, nên cây cối không được xanh tốt và đẹp đẽ như khu rừng của
Quang. Thầy tình trạng khu rừng của mình như vậy, Tùng cảm thấy thật
ghen tị với Quang. Nhưng cũng biết là lỗi của mình không chịu luyện tập,
nên thay vì bắt nạt Quang, Tùng quyết định sẽ thay đổi một phần của khu
rừng của mình để giống với khu rừng của Quang hơn.
Cho cấp bậc của hai vị thần rừng và các cây trong khu rừng của hai vị thần. Hãy giúp vị thần Tùng trả lời ~q~ câu hỏi sau:
Cho ba số ~l~, ~x~ và ~y~. Xét hai khu rừng con sau:
khu rừng
Xtạo bởi ~l~ vị trí liên tiếp trong khu rừngTbắt đầu từ vị trí ~x~,khu rừng
Ytạo bởi ~l~ vị trí liên tiếp trong khu rừngQbắt đầu từ vị trí ~y~.
Liệu có cách nào để biến đổi khu rừng
Xthành khu rừngYsử dụng hai câu thần chú trên một vài lần (có thể là không lần) không?
Lưu ý rằng Tùng đang xét hai khu rừng X và Y riêng biệt. Hai khu
rừng này đều có ~l~ vị trí đánh số từ ~1~ đến ~l~. Vì hai khu rừng không
có vị trí ~l + 1~, nên Tùng cũng không được phép tạo ra cây tại vị trí
này.
Khu rừng X (sau một vài bước biến đổi) và Y được gọi là giống nhau,
nếu như không tồn tại vị trí nào mà trong một khu rừng có cây, nhưng
tại vị trí tương ứng của khu rừng kia lại trống.
Input
Dòng đầu tiên chứa ba số nguyên ~n~, ~k~ và ~q~ (~k < n \le 10^5~, ~1 \le k \le 5~, ~1 \le q \le 10^5~), lần lượt là dộ dài khu rừng của mỗi vị thần, cấp độ của hai vị thần Quang và Tùng, và số lượng câu hỏi mà Tùng đang phân vân.
Dòng tiếp theo chứa xâu ~T~ có độ dài ~n~ là một xâu nhị phân mô tả
khu rừng T. Vị trí thứ ~i~ trong khu rừng T đang có một cây nếu như
~T_i = 1~, ngược lại vị trí này là vị trí rỗng.
Dòng tiếp theo chứa xâu ~Q~ có độ dài ~n~ là một xâu nhị phân mô tả
khu rừng Q. Vị trí thứ ~i~ trong khu rừng Q đang có một cây nếu như
~Q_i = 1~, ngược lại vị trí này là vị trí rỗng.
Mỗi dòng trong ~q~ dòng tiếp theo chứa ba số nguyên ~l~, ~x~ và ~y~ (~k < l \le n~, ~1 \le x, y \le n - l + 1~) là mô tả cho một câu hỏi của vị thần Tùng.
Output
Với mỗi câu hỏi, in ra YES nếu có thể biến đổi khu rừng X (tạo bởi
~l~ cây liên tiếp trong khu rừng T bắt đầu từ vị trí ~x~) thành khu
rừng Y (tạo bởi ~l~ cây liên tiếp trong khu rừng Q bắt đầu từ vị
trí ~y~). Ngược lại, in ra NO.
Scoring
Subtask 1, tương ứng với ~95~ điểm, có ~n, q \le 3000~
Subtask 2, tương ứng với ~215~ điểm, không có giới hạn gì thêm
Tổng cộng bài toán này có ~310~ điểm.
Sample Input 1
8 2 4
00101001
11011110
3 3 2
3 1 6
5 1 4
4 2 3
Sample Output 1
YES
YES
YES
NO
Notes
Ở câu hỏi đầu tiên, hai phần của khu rừng đã giống nhau (đều có dạng
101).
Ở câu hỏi thứ hai, khu rừng X có dạng 001, và khu rừng Y có dạng
110. Ở khu rừng X, ta có thể biến đổi cây ở vị trí ~3~ thành hai cây
ở vị trí ~1~ và ~2~.
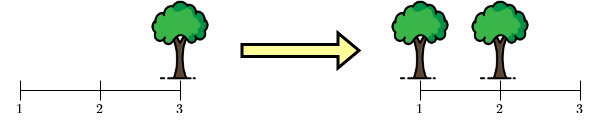
Minh họa phép biến đổi cho câu hỏi thứ hai
Ở câu hỏi thứ ba, khu rừng X có dạng 00101 và khu rừng Y có dạng
11110. Ta có thể thực hiện các biến đổi sau:
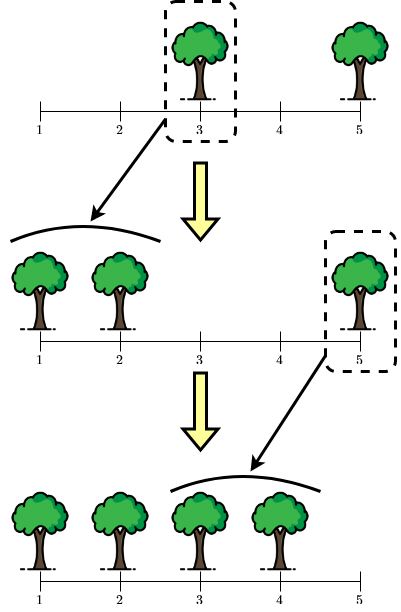
Minh họa phép biến đổi cho câu hỏi thứ ba. Đầu tiên Tùng có thể biến cây tại vị trí ~3~ thành hai câu tại vị trí ~1~ và ~2~. Sau đó biến cây tại vị trí ~5~ thành cây tại vị trí ~3~ và ~4~.
Ở câu hỏi cuối cùng, khu rừng X có dạng 0101, và khu rừng Y có
dạng 0111. Có thể nhận thấy rằng không có cách nào để biến đổi khu
rừng X thành khu rừng Y.
Bình luận