To read the problem statement in English, choose the language using the flag on the navigation bar.

Một đồ thị vô hướng được gọi là quả tạ nếu các đỉnh của nó có thể được chia thành ~2~ phần, trong đó:

• Mỗi cặp đỉnh trong cùng một phần đều có cạnh nối.

• Có chính xác một cạnh nối 2 đỉnh thuộc khác phần nhau.

Các đồ thị dưới đây là các đồ thị quả tạ:

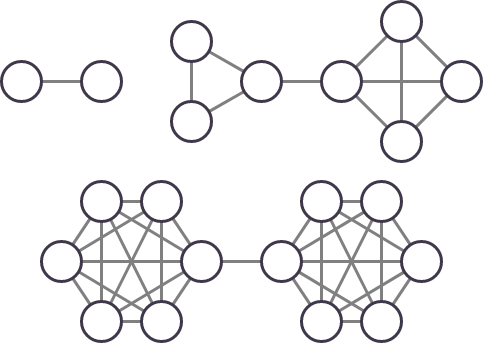
Các đồ thị dưới đây không phải là các đồ thị quả tạ:

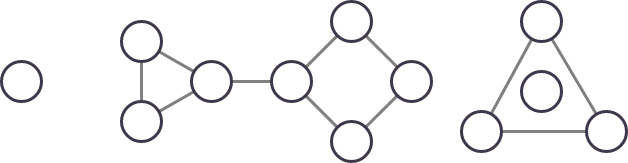
Từ trái qua phải, đồ thị đầu tiên có duy nhất một thành phần liên thông. Đồ thị thứ hai có một phía mà có hai cặp đỉnh không có cạnh nối giữa chúng, và đồ thị thứ ba không liên thông.

Cho một đồ thị vô hướng gồm ~N~ đỉnh và ~M~ cạnh. Đồ thị đã cho không có khuyên và không có nhiều hơn một cạnh nối giữa hai đỉnh bất kì. Hãy tính số lượng cạnh ít nhất cần thêm vào đồ thị để đồ thị trở thành đồ thị quả tạ.

Input

Dòng đầu tiên chứa hai số nguyên ~n~ và ~m~ (~2 \le n \le 10^5~, ~0 \le m \le 10^5~), lần lượt là số lượng đỉnh và cạnh trong đồ thị.

Mỗi dòng trong ~m~ dòng tiếp theo chứa hai số nguyên ~u~ và ~v~ (~1 \le u, v \le n~, ~u \ne v~), thể hiện có một cạnh nối giữa hai đỉnh ~u~ và ~v~.

Dữ liệu đảm bảo mỗi cạnh trong đồ thị xuất hiện duy nhất một lần.

Output

In ra một số nguyên dương duy nhất là số lượng cạnh ít nhất cần thêm vào để đồ thị đã cho trở thành một đồ thị quả tạ.

Nếu không tồn tại cách thêm cạnh nào để tạo ra đồ thị quả tạ, in ra ~-1~.

Scoring

• Subtask 1, ứng với ~125~ điểm, có ~n \le 500~.

• Subtask 2, ứng với ~285~ điểm, không có giới hạn gì thêm.

Tổng cộng bài toán có ~410~ điểm.

Sample Input 1

5 7
2 3
5 3
2 5
2 1
1 5
3 1
5 4

Sample Output 1

0

Sample Input 2

7 5
5 7
2 4
1 3
5 1
5 6

Sample Output 2

5

Sample Input 3

3 3
1 2
2 3
3 1

Sample Output 3

-1