Với đồ họa và cách thức chơi vô cùng đơn giản, trò chơi Flow đang trở nên rất thịnh hành trong thời gian gần đây. Trong bài toán này, chúng ta sẽ cùng nhau thử tìm lời giải cho trò chơi này! Trên một bảng kích thước ~N \times N~, có một số cặp điểm cần được nối với nhau. Như hình vẽ dưới đây, hai ô cùng màu là hai ô cần được nối với nhau.

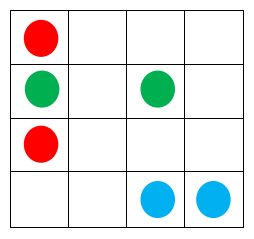
Trên một bảng kích thước ~N \times N~, có một số cặp điểm cần được nối với nhau. Như hình vẽ dưới đây, hai ô cùng màu là hai ô cần được nối với nhau.

Việc nối hai ô bất kì với nhau được thực hiện bằng cách đi theo các ô kề cạnh tạo thành một đường đi không tự cắt (đường đi không được đi qua một ô hai lần) và tới ô đích. Hình ~1~ dưới đây môt tả một đường đi hợp lệ nối hai ô đỏ.

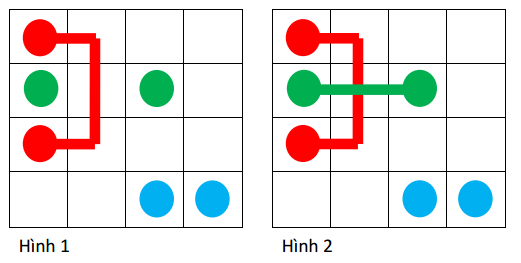
Các đường đi nối các cặp khác điểm khác nhau cũng không được phép có điểm chung với nhau. Hình ~2~ là một cách nối không hợp lệ. Vì vậy với cách nối cặp điểm màu đỏ như hình ~1~, chúng ta không có cách nối cặp điểm màu xanh lá.

Nhiệm vụ của bạn là hãy tìm một phương pháp nối các cặp điểm sao cho:

• Số lượng cặp điểm nối được là nhiều nhất có thể.
• Số lượng ô có đường đi đi qua là nhiều nhất có thể.

Input

• Dòng đầu tiên ghi số ~N~.
• ~N~ dòng tiếp theo, mỗi dòng ghi một xâu ~N~ kí tự mô tả bảng ban đầu. Trong đó ô trống được kí hiệu bởi dấu chấm (.), các ô màu được kí hiệu bởi một chữ cái in hoa.
• Dữ liệu đảm bảo với mỗi màu (chữ cái in hoa) sẽ chỉ có đúng hai ô chứa nó.

Output

In ra bảng gồm ~N \times N~ số mô tả cách nối, trong đó ô ở dòng ~u~, cột ~v~ ghi thông tin về cách nối ở ô (~u~, ~v~). Cách nối ở mỗi ô được mô tả bằng một số nguyên ~X~ trong đó:

• Nếu ô (~u~, ~v~) có nối lên trên thì bít thứ ~0~ (từ phải sang) của ~X~ bằng ~1~.
• Nếu ô (~u~, ~v~) có nối sang phải thì bít thứ ~1~ (từ phải sang) của ~X~ bằng ~1~.
• Nếu ô (~u~, ~v~) có nối xuống dưới thì bít thứ ~2~ (từ phải sang) của ~X~ bằng ~1~.
• Nếu ô (~u~, ~v~) có nối sang trái thì bít thứ ~3~ (từ phải sang) của ~X~ bằng ~1~.

Giới hạn

Bài toán có ~50~ test, mỗi test tối đa ~2~ điểm. Điểm của mỗi test được làm tròn đến ~10~ chữ số sau dấu phẩy, điểm của cả bài là tổng điểm của các test.

Nếu có bất kì một sự không hợp lệ nào trong output (đường đi cắt nhau, hai ô kề nhau không khớp nhau, ô biên nối ra ngoài, có các cạnh nối nhưng không dùng để nối hai điểm ...) bạn sẽ nhận ~0~ điểm. Nếu coi

• ~M~ là số lượng màu khác nhau
• ~X~ là số lượng màu bạn nối được
• ~N^{2}~ là số lượng ô tối đa có thể phủ được.
• ~Y~ là số ô mà bạn phủ được

Điểm của bạn được tính như sau:

• Nếu ~M~ = ~X~ và ~N^{2} = Y~ bạn được ~2~ điểm (dữ liệu luôn đảm bảo có cách làm như vậy)
• Nếu không điểm bạn sẽ được tối đa ~1~. ~5~ điểm. Điểm của bạn bằng: $$Score = 1.5 \times \frac{X \times Y}{M \times N^2}$$

Giới hạn:

• Trong tất cả các test, ~2 \leq N \leq 50~
• Trong 10% số test đầu tiên, chỉ có một cặp điểm phải nối, ~N \leq 50~.
• Trong 20% số test tiếp theo, chỉ có không quá ~4~ cặp điểm phải nối, ~N \leq 50~.
• Trong 30% số test tiếp theo, ~N \leq 15~.
• Trong 40% số test cuối cùng, không có thêm bất kì giới hạn nào.

Sample Input

4
R...
G.G.
R...
..BB

Sample Output

2 10 10 12
2 10 8 5
2 10 10 9
0 0 2 8

Note

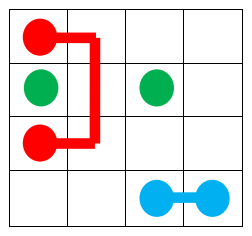
Đây là hình ảnh của output ở ví dụ 1. Với output trên, bạn sẽ được ~1.312500~ điểm. 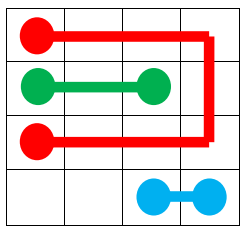Một ouput khác với số điểm là: ~2~

2 10 10 12
2 10 8 5
4 6 10 9
3 9 2 8

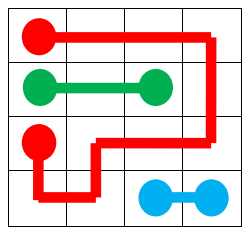Một output khác với số điểm là: ~0.437500~

2 12 0 0
0 5 0 0
2 9 0 0
0 0 2 8