Để chào mừng đại lễ kỉ niệm ~1000~ năm Thăng Long Hà Nội, bạn bè trên khắp thế giới đã quyết định góp ~Q~ phiến đá quý ~(1 \leq 30\,000 \leq Q)~ giúp thủ đô xây dựng một tòa tháp gồm ~K~ tầng ~(1 \leq K \leq Q)~, mỗi tầng làm từ một phiến đá quý. Những phiến đá này có hình dạng và kích thước giống hệt nhau, nhưng lại có "độ quý" ~C~ khác nhau ~(1 \leq C \leq 10\,000)~.

Đá quý được tập kết về thủ đô thành ~M~ chồng xếp liền nhau theo một hàng dài, chồng đá thứ ~i~ gồm ~H_i~ phiến đá (~H_i > 0~, và do kích thước các phiến đá là như nhau nên cũng có thể coi ~H_i~ là "chiều cao" của chồng đá thứ ~i)~.

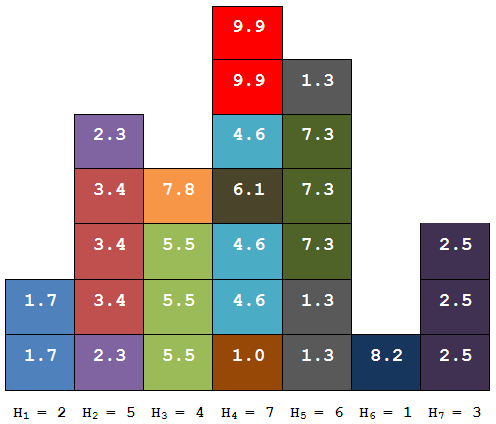
Sau đó các phiến đá lần lượt được "gắp" vào công trường để xây dựng tòa tháp (xây từ dưới lên trên) bằng một chiếc cần cẩu chuyên dụng (chiếc loại ~I)~. Chiếc ngoàm của cần cẩu được thiết kế chỉ có thể gắp mỗi lượt một phiến đá đang nằm trên cùng của một chồng đá bất kì, với điều kiện hai chồng đá liền kề phải có chiều cao nhỏ hơn chiều cao của chồng đó (nếu phía bên nào không có đá thì coi như chồng bên đó có chiều cao bằng ~0)~. Để khắc phục nhược điểm đó, có một chiếc cần cẩu khác (chiếc loại II) được thiết kế đặc biệt có thể gắp bất kì phiến đá nào (tất nhiên phải là phiến đá nằm trên cùng của một chồng, và cũng chỉ có thể gắp mỗi lượt một phiến); tuy nhiên chiếc cần cẩu này lại làm "xước" phiến đá mà nó gắp, nên độ quý của phiến đá đó chỉ còn là ~C \times P\%~ ~(0 < P < 100)~.

Mặt khác, do các phiến đá cùng loại nếu được đặt chồng lên nhau sẽ tạo ra "hiệu ứng ánh sáng" rất đẹp mắt nên khi đó độ quý của phiến đá nằm trên sẽ tăng so với độ quý của phiến đá nằm dưới là ~D\%~ ~(D > 0)~, nếu phiến đá nằm trên bị xước (do sử dụng cần cẩu loại II) thì độ quý của phiến đá sau khi tăng ~D\%~ mới được nhân với ~P\%~ để nhận được độ quý cần tính.

Tổng độ quý ~S~ của tòa tháp là tổng các độ quý của ~K~ phiến đá tạo nên tòa tháp theo cách tính nói trên. Vấn đề đặt ra là hãy lựa chọn một phương án xây tháp sao cho ~S~ càng lớn càng tốt!

Input

• Dòng đầu tiên chứa ~5~ số nguyên ~N~, ~M~, ~K~, ~P~, ~D~ trong đó ~N~ là số loại đá khác nhau (các loại đá được đánh số từ ~1~ ...~N)~.

• Dòng thứ hai chứa ~N~ số thực ~R_i~ là độ quý của loại đá thứ ~i~ ~(i = 1~ ...~N)~.

• ~M~ dòng cuối cùng, dòng thứ ~j~ ~(j = 1~ ...~M)~ có định dạng:

  • Bắt đầu bằng số nguyên ~H~ là số phiến đá ở chồng đá thứ ~j~.
  • Tiếp theo là ~H~ số nguyên ~T_v~ ~(v = 1~ ...~H)~ với ý nghĩa phiến đá thứ ~v~ (tính từ dưới lên) thuộc chồng đá thứ ~j~ là loại đá ~T_v~ ~(T_v = 1~ ...~N)~.

Output

• Ghi ra trên ~K~ dòng, dòng thứ ~i~ ~(i = 1~ ...~K)~ ghi số nguyên ~L_i~ ~(L_i = 1~ ...~M)~ thể hiện: lần gắp thứ ~i~ (theo thứ tự thời gian) chọn gắp phiến đá trên cùng của chồng đá thứ ~L_i~.

Các cần cẩu sẽ được sử dụng theo nguyên tắc: ưu tiên sử dụng cần cẩu loại ~I~, trong trường hợp một trong các điều kiện để sử dụng cần cẩu loại ~I~ không được thỏa mãn thì sẽ sử dụng đến chiếc cần cẩu loại II.

Giới hạn

• Số điểm bạn nhận được sẽ tỉ lệ với tổng độ quý ~S~ của tòa tháp bạn xây được.
• Gọi ~S_1~ là độ quý ~S~ của BTC, ~S_2~ là độ quý của bạn, ~T~ là điểm của test. Điểm bạn nhận được trong test đó là ~\min\left(\frac{S_2}{S_1} \times T \times 95\%, T\right)~

Sample Input

13 7 7 70 30
1.7 2.3 3.4 5.5 7.8 1.0 4.6 6.1 9.9 1.3 7.3 8.2 2.5
2 1 1
5 2 3 3 3 2
4 4 4 4 5
7 6 7 7 8 7 9 9
6 10 10 11 11 11 10
1 12
3 13 13 13

Sample Output

4
4
5
4
5
5
5

Note

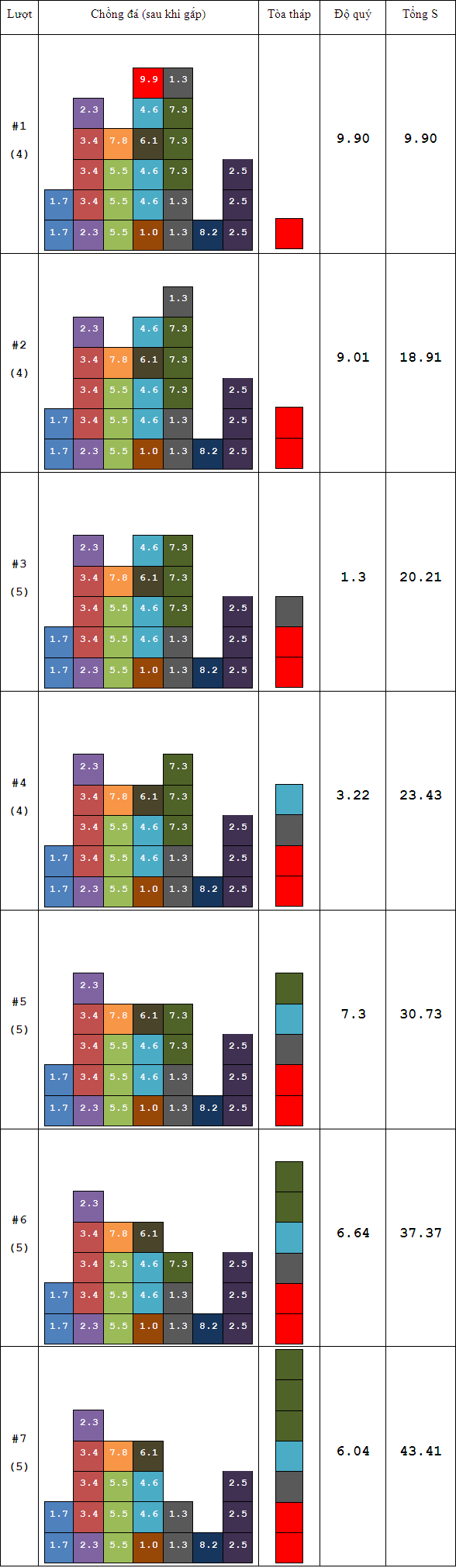
Như vậy với phương án xây tháp này bạn sẽ nhận được ~S = 43.41~

Một phương án khác với thứ tự gắp lần lượt là ~4~, ~4~, ~5~, ~4~, ~4~, ~5~, ~5~ sẽ cho ~S = 44.49~