Tổ chức đối lập
Xem dạng PDFỞ một đất nước nọ, lực lượng an ninh vừa phát hiện một tổ chức đối lập. Tổ chức đối lập này được tổ chức chặt chẽ, bao gồm mạng lưới thành viên và chỉ huy ở các cấp bậc khác nhau. Các thành viên của tổ chức được đánh số từ ~1~ đến ~N~. Tổ chức có một chỉ huy tối cao, luôn được đánh số 1. Mỗi thành viên chỉ biết viên chỉ huy trực tiếp của mình (có duy nhất một viên chỉ huy trực tiếp) chứ không biết các chỉ huy cấp cao hơn.
Khi tiến hành việc bắt giữ các thành viên, tổ chức sẽ bị phân rã thành các nhóm nhỏ không liên kết với nhau, ví dụ sau khi bắt giữ thành viên số ~2~ (hình dưới), tổ chức bị phân rã thành ~4~ nhóm. Lực lượng an ninh khẳng định, một nhóm chứa ít hơn ~K~ thành viên sẽ không còn là mối đe dọa cho đất nước. Để không làm giảm hình ảnh của đất nước trước dư luận quốc tế, các nhà lãnh đạo an ninh muốn bắt giữ một số lượng ít nhất phần tử đối lập, sao cho các nhóm bị phân rã đều không còn gây nguy hại cho đất nước.
Cho biết cấu trúc của tổ chức đối lập, việc chương trình giúp các nhà lãnh đạo an ninh xác định số lượng phần tử đối lập ít nhất cần bắt giữ.
Input
- Dòng đầu tiên chứa số nguyên ~K~ ~(1 \le K \le 10000)~.
- Dòng thứ hai chứa số nguyên ~N~ ~(1 \le N \le 10000)~.
- Dòng thứ ba chứa ~N-1~ số nguyên cách nhau bởi khoảng trắng, chỉ số của chỉ huy trực tiếp của mỗi phần tử của tổ chức (trừ chỉ huy tối cao): số đầu tiên cho biết chỉ huy của phần tử thứ hai, số thứ hai cho biết chỉ huy của phần tử thứ ba, ...
Output
- In ra một số nguyên duy nhất là số phần tử đối lập ít nhất cần bắt giữ.
Sample Input
3
14
1 1 2 2 3 2 3 6 6 6 7 4 7
Sample Output
4
Note
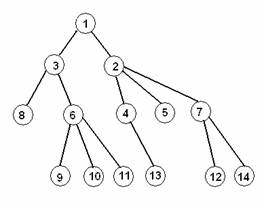
- Có thể bắt giữ ~4~ phần tử ~6~, ~2~, ~7~ và ~8~.
Bình luận
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.
bai hay qa