Bessie có ~N~ ~(3 \le N \le 40)~ điểm ưa thích phân biệt đôi một trên một mặt phẳng hai chiều, với bất kì ba điểm nào trên mặt phẳng không thẳng hàng. Với mỗi ~1 \le i \le N~, tọa độ của điểm thứ ~i~ được biểu diễn bằng hai số nguyên ~x_i~ và ~y_i~ ~(0 \le x_i, y_i \le 10^4)~.

Bessie vẽ một số đoạn thẳng giữa các điểm như sau:

1. Chọn một hoán vị bất kì ~p_1, p_2, \ldots, p_N~ của ~N~ điểm đã cho.
2. Vẽ các đường thẳng nối các điểm ~p_1~ và ~p_2~, ~p_2~ và ~p_3~, ~p_3~ và ~p_1~.
3. Sau đó, với mỗi ~i~ từ ~4~ tới ~N~ theo thứ tự, bạn ấy vẽ một đoạn thẳng từ ~p_i~ với ~p_j~ với mọi ~j < i~ sao cho đoạn thẳng đó không giao với bất kì đoạn thẳng nào đã được vẽ từ trước (ngoại trừ tại các đầu mút).

Bessie nhận thấy rằng với mỗi ~i~, bạn ấy đã vẽ đúng ba đoạn thẳng. Hãy đếm số lượng hoán vị mà Bessie có thể chọn ở bước 1 để thỏa mãn điều kiện này, modulo ~10^9 + 7~.

Input

Dòng đầu chứa số nguyên ~N~.

~N~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~x_i~ và ~y_i~ cách nhau bởi một dấu cách.

Output

In ra số hoán vị thỏa mãn modulo ~10^9 + 7~.

Sample Input 1

4
0 0
0 4
1 1
1 2

Sample Output 1

0

Giải thích: Không có bất kì hoán vị nào thỏa mãn điều kiện đề bài.

Sample Input 2

4
0 0
0 4
4 0
1 1

Sample Output 2

24

Giải thích: Mọi hoán vị đều thỏa mãn điều kiện đề bài.

Sample Input 3

5
0 0
0 4
4 0
1 1
1 2

Sample Output 3

96

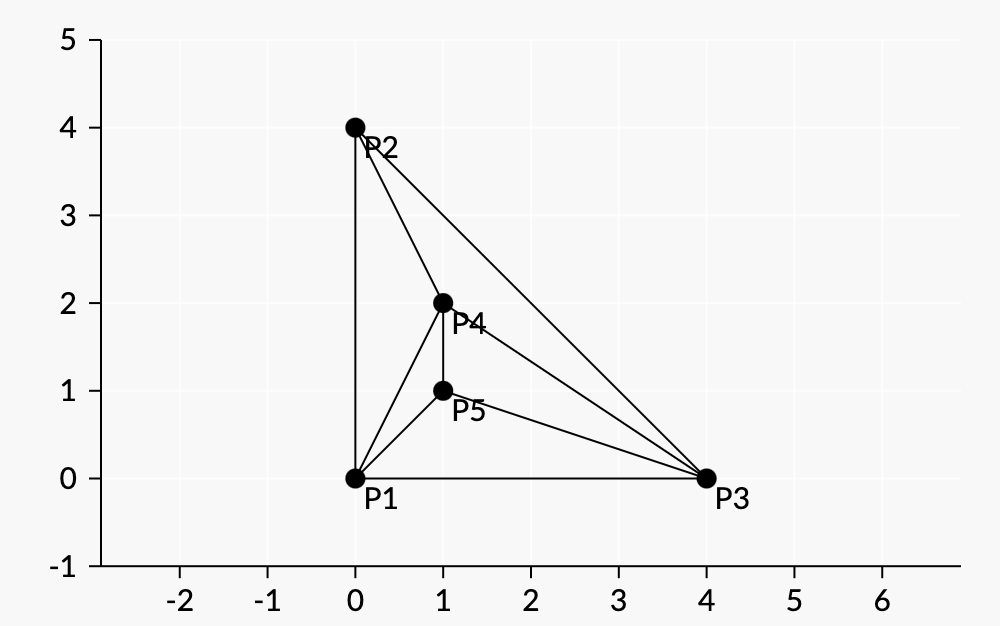
Giải thích: Một hoán vị thỏa mãn điều kiện đề bài là ~(0,0),(0,4),(4,0),(1,2),(1,1)~

Các đoạn thẳng được vẽ theo thứ tự như sau:

• Đầu tiên, vẽ các đoạn thẳng giữa từng cặp điểm của ba điểm đầu tiên ~(0,0),(0,4),~ và ~(4,0)~.
• Tiếp theo, vẽ các đoạn thẳng từ ~(1,2)~ đến ~(0,0), (0,4),~ và ~(4,0)~.
• Cuối cùng, vẽ các đoạn thẳng từ ~(1, 1)~ đến ~(1,2), (4,0),~ và ~(0,0)~.

Hình vẽ:

Ràng buộc

• Các test 1-6 thỏa mãn ~N \le 8~.
• Các test 7-20 không có thêm ràng buộc nào.