VOI 11 Bài 6 - Nâng cấp mạng
Xem dạng PDFMột hệ thống gồm ~n~ máy tính đánh số từ ~1~ đến ~n~ được kết nối thành một mạng bởi ~m~ đoạn cáp mạng đánh số từ ~1~ đến ~m~. Đoạn cáp mạng thứ ~i~ có thông lượng ~w_{i}~ kết nối hai máy ~u_{i}~ , ~v_{i}~ cho phép truyền dữ liệu theo cả hai chiều giữa hai máy này.
Một dãy các máy ~x_{1} , x_{2} , ..., x_{p}~ trong đó giữa hai máy ~x_{j}~ và ~x_{j+1} \;(j = 1, 2, ..., p-1)~ có đoạn cáp nối được gọi là một đường truyền tin từ máy ~x_{1}~ tới máy ~x_{p}~ . Thông lượng của đường truyền tin được xác định như là thông lượng nhỏ nhất trong số các thông lượng của các đoạn cáp mạng trên đường truyền. Giả thiết là mạng được kết nối sao cho có đường truyền tin giữa hai máy bất kì và giữa hai máy có không quá một đoạn cáp mạng nối chúng.
Người ta muốn nâng cấp mạng bằng cách tăng thông lượng của một số đoạn cáp nối trong mạng. Để tăng thông lượng của mỗi đoạn cáp mạng thêm một lượng ~d \;(d > 0)~ ta phải trả một chi phí đúng bằng ~d~. Việc nâng cấp mạng phải đảm bảo là sau khi hoàn tất, thông lượng của mỗi đoạn cáp mạng ~i~ đều bằng thông lượng của đường truyền tin có thông lượng lớn nhất từ máy ~u_{i}~ tới máy ~v_{i}~ .
Yêu cầu: Tìm phương án nâng cấp các đoạn cáp mạng sao cho tổng chi phí nâng cấp là nhỏ nhất.
Input
- Dòng thứ nhất: Chứa hai số nguyên dương ~n, m \;(n, m \leq 10^5)~.
- Dòng thứ ~i~ trong số ~m~ dòng tiếp theo chứa ba số nguyên dương ~u_{i} , v_{i} , w_{i}\; (w_{i} \leq 10^6), \;i = 1, 2, ..., m~.
Các số trên cùng một dòng được ghi cách nhau ít nhất một dấu cách.
Output
Ghi ra một số nguyên duy nhất là tổng chi phí nâng cấp theo phương án tìm được.
Giới hạn
50% số test ứng với 50% số điểm của bài có ~n \leq 100~.
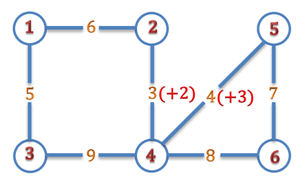
Sample Input
6 7
1 2 6
1 3 5
2 4 3
3 4 9
4 5 4
4 6 8
5 6 7
Sample Output
5
Note
Bình luận
Skibidi toilet
đề voi khó hiểu vaiz :)
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.