TST 2023 - Bài 1
Xem dạng PDFHệ thống đường nước thành phố gồm ~N~ trạm được đánh số từ ~0~ đến ~N - 1~ và ~N - 1~ đoạn ống tròn nối giữa các trạm được đánh số từ ~0~ đến ~N - 2~. Giữa hai trạm bất kỳ luôn tồn tại một đoạn ống nối trực tiếp hoặc một dãy đoạn ống liên tiếp dẫn tới nhau thông qua các trạm trung gian. Đoạn ống thứ ~i~ (~0 \le i \le N - 2~) có đường kính là ~D_i~ (mét).
Gọi ~D_{min}~(~x, y~) là đường kính nhỏ nhất trong các đoạn ống nối từ trạm ~x~ đến trạm ~y~ bằng con đường đi qua ít đoạn ống nối nhất, khi đó:
Chi phí thi công để nước có thể đi vào từ trạm vào ~w~ và đi ra ở trạm ra ~u~ được tính bằng: ~D_{min}(w, u) \cdot H~, với ~H~ là hệ số chi phí.
Đối với một trạm vào ~w~ và hai trạm ra ~u~ và ~v~ (~w \neq u~, ~w \neq v~, ~u~ và ~v~ có thể trùng nhau), chi phí thi công là: ~f(w, u, v) = \max(D_{min}(w, u) \cdot H, D_{min}(w, v) \cdot H)~.
Với một chi phí đầu tư ~c~ và hai trạm ra ~u~ và ~v~, Ban quản lý hệ thống đường nước muốn tìm ra tập ~S~ gồm nhiều nhất các trạm vào sao cho ~\sum_{w \in s} f(w, u, v) \le c~ và ~u, v \notin S~.
Yêu cầu: Hãy giúp ban quản lý trả lời ~Q~ câu hỏi như trên.
Chi tiết cài đặt
Thí sinh cần cài đặt hai hàm sau:
void init(const vector<int> &A, const vector<int> &B, const vector<int> &D, int H)
Hàm nhận vào các tham số mô tả hệ thống đường nước;
~H~: hệ số chi phí;
~A~, ~B~, ~D~: các vector chứa ~n - 1~ phần tử, với mỗi số nguyên ~i~ (~0 \le i \le n - 2~), có một đoạn ống nối trực tiếp hai trạm ~A[i]~ và ~B[i]~ với đường kính ~D[i]~.
Hàm này được gọi đúng một lần, trước bất kỳ lệnh gọi nào đến hàm query.
int query(int u, int v, long long c)
Hàm nhận vào ba tham số ~u~, ~v~ và ~c~ mô tả một câu hỏi;
Hàm cần trả về một số nguyên không âm là số lượng phần tử của tập ~S~, nghĩa là số lượng trạm vào nhiều nhất tìm được sao cho ~\sum_{w \in s} f(w, u, v) \le c~ và ~u, v \notin S~.
Hàm này được gọi đúng ~Q~ lần.
Trình chấm mẫu
Tải trình chấm mẫu tại đây.
Trình chấm mẫu đọc dữ liệu vào theo định dạng:
dòng ~1~: ~N~ ~Q~ ~H~
dòng ~2 + i~ (~0 \le i \le N - 2~): ~A[i]~ ~B[i]~ ~D[i]~
dòng ~n + 1 + j~ (~0 \le j \le Q - 1~): ~u~ ~v~ ~c~ với câu hỏi ~j~
Trình chấm mẫu in các kết quả của bạn theo định dạng:
- dòng ~1 + j~ (~0 \le j \le Q - 1~): giá trị trả về của query cho câu hỏi ~j~
Ràng buộc
~1 \le N \le 25 \cdot 10^4~, ~1 \le Q \le 75 \cdot 10^4~, ~1 \le H \le 2023~.
Các tham số truyền vào hàm init thỏa mãn ~0 \le A[i], B[i] \le N - 1~ và ~1 \le D[i] \le 10^9~.
Các tham số truyền vào hàm query thỏa mãn ~0 \le u, v \le N - 1~ và ~1 \le c \le 10^{18}~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~6~ | ~N \le 5000~ và ~Q \le 1000~ |
| 2 | ~19~ | ~D[i] \le 20~ |
| 3 | ~22~ | Trong tất cả các lần gọi hàm query, ~u = v~. |
| 4 | ~20~ | Mỗi trạm được nối trực tiếp tới không quá hai trạm khác. |
| 5 | ~18~ | ~Q \le 200000~ |
| 6 | ~15~ | Không có ràng buộc gì thêm. |
Sample Input 1
6 4 1
0 1 2
0 2 4
0 3 3
3 4 1
3 5 2
4 5 7
0 4 6
1 2 8
3 3 11
Sample Output 1
3
2
3
5
Notes
Dưới đây là một ví dụ về việc gọi hàm:
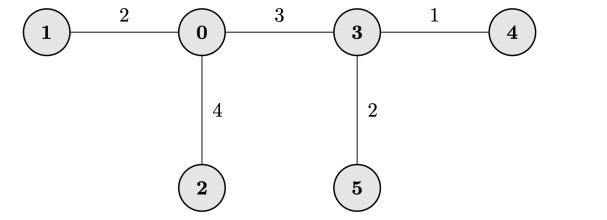
init([0, 0, 0, 3, 3], [1, 2, 3, 4, 5], [2, 4, 3, 1, 2], 1)
Hàm khởi tạo hệ thống đường nước giống như mô tả ở hình bên dưới.
query(4, 5, 7)
Hàm trả về ~3~, một tập ~S~ gồm nhiều trạm nhất thỏa mãn là ~\{0,1,2\}~, khi đó: ~f(0,4,5)=2~; ~f(1,4,5)=2~; ~f(2,4,5) = 2~.
query(0, 4, 6)
Hàm trả về ~2~, một tập ~S~ gồm nhiều trạm nhất thỏa mãn là ~\{1,2\}~, khi đó ~f(1,0,4)=2~; ~f(2,0,4)=4~.
query(1, 2, 8)
Hàm trả về ~3~, một tập ~S~ gồm nhiều trạm nhất thỏa mãn là ~\{0,3,4\}~, khi đó: ~f(0,1,2)=4~; ~f(3,1,2)=3~; ~f(4,1,2)=1~.
query(3, 3, 11)
Hàm trả về ~5~, tập ~S~ gồm nhiều trạm nhất thỏa mãn là ~\{0,1,2,4,5\}~.

Bình luận
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.