Hãy chia hình chữ nhật kích thước ~10^6 \times 10^6~ thành các hình chữ nhật nhỏ hơn bằng các đường thẳng dọc, tạo ra ~1,000~ hình chữ nhật kích thước ~10^3 \times 10^6~.

Đánh số chúng từ trái sang phải. Ta sẽ di chuyển qua các điểm từ hình chữ nhật này sang hình chữ nhật khác. Trong cùng một hình chữ nhật, ta sẽ đi qua các điểm theo thứ tự tăng dần của tọa độ ~y~ nếu số của hình chữ nhật đó là số chẵn, và ngược lại nếu là số lẻ.

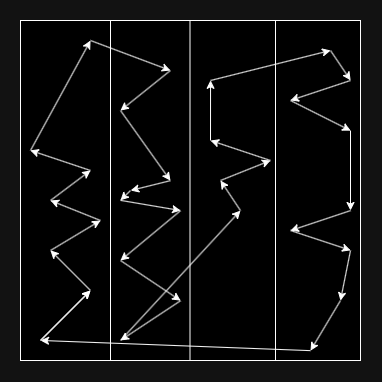
Chứng minh tính đúng đắn: Tính chiều dài lớn nhất của một con đường theo cách này.

Các tọa độ là độc lập.

Theo tọa độ ~y~, đi qua ~1,000~ hình chữ nhật từ ~0~ đến ~10^6~, tổng cộng là ~10^9~ đơn vị.

Theo tọa độ ~x~, chúng ta mất ~1,000~ để đến điểm kế tiếp trong cùng một hình chữ nhật và ~2,000~ để đến hình chữ nhật tiếp theo.

Tổng cộng là ~2 \times 10^9 + 2,000,000~.

Độ phức tạp: ~O(n \times log(n))~.