VOI 06 Bài 1 - Chọn ô - VNOJ: VNOI Online Judge

VOI 06 Bài 1 - Chọn ô

View as PDF

Submit solution

All submissions

Read editorial

Points: 0.04 (partial)

Time limit: 0.38s

Memory limit: 512M

Input: stdin

Output: stdout

Problem source:

Vietnam Olympiad of Informatics 2006 - Bảng B

Problem type

Allowed languages

C, C++, Go, Java, Kotlin, Pascal, PyPy, Python, Rust, Scratch

Cho một bảng hình chữ nhật kích thước ~4×n~ ô vuông. Các dòng được đánh số từ 1 đến 4, từ trên xuống dưới, các cột được đánh số từ 1 đến n từ trái qua phải.

Ô nằm trên giao của dòng i và cột j được gọi là ô ~(i,j)~. Trên mỗi ô ~(i,j)~ có ghi một số nguyên ~a_{i,j}~, ~i = 1, 2, 3, 4;~ ~j = 1, 2, \dots, n~. Một cách chọn ô là việc xác định một tập con khác rỗng ~S~ của tập tất cả các ô của bảng sao cho không có hai ô nào trong ~S~ có chung cạnh. Các ô trong tập ~S~ được gọi là ô được chọn, tổng các số trong các ô được chọn được gọi là trọng lượng của cách chọn. Tìm cách chọn sao cho trọng lượng là lớn nhất.

Ví dụ: Xét bảng với ~n = 3~ trong hình vẽ dưới đây:

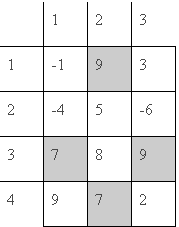
Cách chọn cần tìm là tập các ô ~S = \{(3,1), (1,2), (4,2), (3,3)\}~ với trọng lượng 32.

Input

Dòng đầu tiên chứa số nguyên dương n là số cột của bảng.

Cột thứ j trong số n cột tiếp theo chứa 4 số nguyên ~a_{1,j}~ , ~a_{2j,}~ , ~a_{3,j}~ , ~a_{4,j}~, hai số liên tiếp cách nhau ít nhất một dấu cách, là 4 số trên cột j của bảng.

Output

Gồm 1 dòng duy nhất là trọng lượng của cách chọn tìm được.

Giới hạn

Trong tất cả các test: ~n \leq 10\,000~, ~|a_{i,j}| \leq 30\,000~.

Có 50% số lượng test với ~n \leq 1000~.

Sample Input

Sample Output

Comments

Comments

Please read the guidelines before commenting.

2

hoangquys commented on Feb. 9, 2026, 3:06 p.m.

Test 15 sai thì hãy nghĩ đến trường hợp mảng full âm nhe

3

ngoannam123456789 commented on Dec. 21, 2025, 4:01 p.m.

Hint

dp 5 chiều cho những trường hợp mà các cạnh không kề.

Solve

Tạo 1 mảng 5 chiều dp[hang][a1][a2][a3][a4] (a, a2, a3, a4 là trạng thái của cột = 0 nếu không nhận, = 1 nếu nhận ).

Xếp lại Input theo a[hang][cot] ( cot <= 4 ).

dp[i][a1][a2][a3][a4] là giá trị lớn nhất nếu lấy giá trị ở [a1][a2][a3][a4] tại hàng i

Nhứng trạng thái bao gồm 0000, 1000, 0100, 0010, 0001, 1010, 1001, 0101.

d[i][0][0][0][1] = max
({
y[i][4],
y[i][4] + d[i-1][1][0][0][0],
y[i][4] + d[i-1][0][1][0][0],
y[i][4] + d[i-1][0][0][1][0],
y[i][4] + d[i-1][1][0][1][0],
y[i][4] + d[i-1][0][0][0][0]
}); ....tt

Chú ý nếu không chọn là max thì ans = max của a[i][j].

Cho ai muốn kiểm tra kq

demo

1

DAThinh_HuMaDa commented on Jan. 22, 2026, 7:00 a.m.

thank NAN

vominhmanh10 commented on Nov. 17, 2025, 2:24 p.m. ← edit 11 →

thì mik qhđ các trạng thái là cột i và tập chọn mask => dp[i][mask] mã bị ngược thành dp[mask][i]
để nhanh nên gom các mask hợp lệ của 1 cột để duyệt nhanh, tính mảng cộng dồn cho mỗi cột mỗi mask
kiểm tra 2 cột(mask i, j) ko trùng hàng bằng i & j == 0
lưu ý đề yêu cầu chọn tập con khác rỗng nên không được phép có chuyện không chọn gì cả, trường hợp này chọn phần tử lớn nhất là xong

import sys
input = sys.stdin.readline

def solve():
    n = int(input())
    a = [list(map(int, input().split())) for _ in range(4)]
    mask = [0, 1, 2, 4, 5, 8, 9, 10]
    pre = [[0] * n for _ in range(11)]
    maxa = -10**18
    for i in range(4): 
        for j in range(n): maxa = max(a[i][j], maxa) 
    for i in range(n):
        for j in mask:
            for k in range(4):
                if (j >> k) & 1: pre[j][i] += a[k][i]
    dp = [[-10**18] * n for _ in range(11)]
    for j in mask:
        dp[j][0] = pre[j][0]
    for i in range(1, n):
        for j in mask:
            for k in mask:
                if not (j & k): dp[j][i] = max(dp[j][i], dp[k][i - 1] + pre[j][i])
    res = -10**18
    for j in mask:
        res = max(dp[j][n - 1], res)
    if res != 0: print(res)
    else: print(maxa)
solve()

-1

haiduong151109 commented on June 22, 2025, 10:41 a.m.

https://ideone.com/nm23so code e sai đâu v ạ ?

1

truonghovuviet commented on July 15, 2025, 7:38 a.m.

Phải chọn ít nhất 1 ô.

-13

phannam310810 commented on June 17, 2025, 1:33 a.m.

trau van ac dcm

This comment is hidden due to too much negative feedback. Show it anyway.

-17

phannam310810 commented on May 10, 2025, 3:30 p.m.

mmb

This comment is hidden due to too much negative feedback. Show it anyway.

-2

Thanh09 commented on April 1, 2025, 7:01 a.m. ← edited →

ban em comment, em xin loi moi nguoi a...

-11

tiendungnguyen860 commented on April 1, 2025, 8:47 a.m.

một diễn đàn học tập lớn như vậy mà bạn có phát ngôn một cách thô thiển vậy sao ?!?!

This comment is hidden due to too much negative feedback. Show it anyway.

-7

kqhuy123 commented on April 1, 2025, 8:42 a.m.

cẩn thận bị ban nha bạn

This comment is hidden due to too much negative feedback. Show it anyway.

-8

ThanhPhong commented on April 1, 2025, 7:10 a.m.

tuc tiu qua, thu hoi tin nhan di b

This comment is hidden due to too much negative feedback. Show it anyway.

-9

ThanhBC1234 commented on Feb. 24, 2025, 7:47 a.m. ← edited →

dp bitmask

This comment is hidden due to too much negative feedback. Show it anyway.

-5

minhtuanvp2011 commented on Feb. 23, 2025, 3:51 p.m. ← edited →

ko co j

This comment is hidden due to too much negative feedback. Show it anyway.

-6

nehuy7410 commented on Nov. 28, 2024, 12:50 p.m.

.

This comment is hidden due to too much negative feedback. Show it anyway.

30

huynhquocluatit10 commented on April 13, 2024, 8:48 a.m. ← edited →

gợi ý:có trường hợp full âm nha

0

minha2k25cvp commented on Oct. 9, 2024, 2:58 p.m.

bạn có test khong ạ, mình vãn bị sai 1 test

-8

duonggiabao2008 commented on April 13, 2024, 8:52 a.m.

Cảm ơn bạn nhé!!!

This comment is hidden due to too much negative feedback. Show it anyway.

-92

tonblan commented on March 17, 2024, 6:15 p.m.

hãy giúp tôi có contribution point thấp nhất vnoi

This comment is hidden due to too much negative feedback. Show it anyway.

-22

hieuhfgr commented on March 19, 2024, 8:21 a.m.

ok

This comment is hidden due to too much negative feedback. Show it anyway.

-38

nogo007akapkn commented on Nov. 8, 2023, 2:28 a.m. ← edit 3 →

tron viet nam

This comment is hidden due to too much negative feedback. Show it anyway.