Cho một bảng hình chữ nhật kích thước ~m×n~ ô vuông kích thước đơn vị. Các dòng được đánh số từ 1 đến ~m~, từ trên xuống dưới. Các cột được đánh số từ 1 đến ~n~, từ trái qua phải.

Mỗi ô của bảng hoặc được để trống hoặc chứa một ký tự lấy từ tập ~S~ gồm các chữ số từ 0 đến 9 và các chữ cái la tinh in hoa từ 'A' đến 'Z'. Hai ô chứa cùng một ký tự được gọi là giống nhau. Mỗi ký tự của tập ~S~ xuất hiện ở không quá 4 ô trong bảng.

Hai ô giống nhau có thể xoá được nếu chúng có cạnh chung hoặc có thể nối các tâm (giao điểm của hai đường chéo) của chúng với nhau bằng một đường gấp khúc gồm không quá 3 đoạn thẳng độ dài nguyên, mỗi đoạn song song với cạnh của bảng và ngoại trừ hai ô cần xoá, đường gấp khúc chỉ qua các ô trống hay nằm ngoài bảng. Các ô bị xoá trở thành ô trống. Mỗi lần xoá một cặp ô của bảng được gọi là một bước.

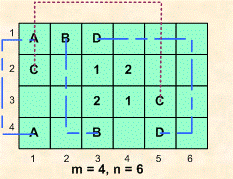
Hình bên trên nêu ví dụ với trường hợp ~m = 4~ và ~n = 6~. Bước đầu tiên có thể xoá hai ô chứa ký tự 'A', tiếp theo, lần lượt xoá các cặp ô chứa 'B', chứa 'C' và cặp ô chứa 'D'. Ở ví dụ này, sau khi thực hiện 4 bước xoá có thể, trong bảng còn lại 4 ô không thể xoá được.

Yêu cầu: Cho ~m~, ~n~ và ~m~ xâu độ dài ~n~ mô tả các dòng của bảng. Hãy xác định số lượng ô lớn nhất có thể xoá được.

Input

Dòng đầu tiên chứa 2 số nguyên ~m, n~ được ghi cách nhau bởi dấu cách.

Dòng thứ ~i+1~ chứa xâu ~n~ ký tự mô tả dòng thứ ~i~ của bảng ~(i = 1, 2, \dots, m)~. Các ô trống được thể hiện bằng dấu chấm ('.').

Output

Gồm một số nguyên duy nhất là số lượng ô lớn nhất có thể xoá được.

Giới hạn

Trong tất cả các test: ~0 < m \leq 10~, ~0 < n \leq 10~. Có 60% số lượng test có ~m \leq 5~, ~n \leq 6~ và số lượng các ô khác trống không quá ????.

Sample Input

4 6
ABD...
C.12..
..21C.
A.B.D.

Sample Output

8