Bạn được cho ~1~ cây (đồ thị liên thông không chu trình), và các cạnh của cây vì lí do nào đó đã được định chiều; nhiệm vụ của bạn là thêm vào ít nhất các đường đi đặc biệt trên cây này sao cho có thể đi từ mọi đỉnh đến mọi đỉnh khác. Luật của các đường đi đặc biệt như sau:

1. Một đường đi đặc biệt gồm một số cạnh và đỉnh liên tiếp trên cây.
2. Trong đường đi đặc biệt, các cạnh được định hướng ngược lại so với cạnh tương ứng trên cây.
3. Một đỉnh hoặc một cạnh chỉ được thăm tối đa ~1~ lần trong ~1~ đường đi đặc biệt.
4. Nhiều đường đi đặc biệt có thể có chung đỉnh hoặc canh.

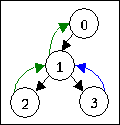
Ví dụ, trong hình dưới đây là một cây, mũi tên đen mô tả cạnh và hướng của nó, hình tròn mô tả đỉnh. Ta có ~2~ đường đi đặc biệt. Một đường là ~2 - 1 - 0~ (mũi tên xanh lá cây), và đường kia là ~3 - 1~ (mũi tên xanh lam). Thay vì đường ~3 - 1~ ta có thể dùng ~3 - 1 - 0~. Bạn không thể dùng đường ~1 - 3~ hay ~0 - 1 - 2~ vì vi phạm luật thứ ~2~. Bạn không thể dùng đường ~0 - 2~ hoặc ~2 - 3 - 0~ vì vi phạm luật thứ ~1~.

Input

Dữ liệu bắt đầu bằng một số nguyên ~T~ ~(\leq 30)~, thể hiện số lượng bộ test.

Mỗi bộ test bắt đầu bằng một dòng chứa số nguyên ~N~ ~(2 \leq N \leq 20000)~, mô tả số lượng đỉnh. Các đỉnh được đánh số từ ~0~ đến ~N - 1~. Mỗi dòng trong số ~N - 1~ dòng tiếp theo chứa ~2~ số nguyên ~u v~ ~(0 \leq u~, ~v < N~, ~u \neq v)~ mô tả một cạnh từ ~u~ đến ~v~.

Output

Với mỗi bộ test, in ra chỉ số của bộ test và số lượng đường đi đặc biệt ít nhất cần thêm vào sao cho có thể đi lại giữa ~2~ đỉnh bất kỳ.

Sample Input

2 
4 
0 1
1 2 
1 3 
5 
0 1 
1 2 
1 3 
0 4

Sample Output

Case 1: 2
Case 2: 3