Gần ngôi làng có một hang động tổ tiên của Mirko đã sống hàng nghìn năm về trước. Muốn là người đầu tiên phát hiện ra những di vật cổ đại này, Mirko chuẩn bị cho chuyến đi khám phá hang động. Do hang động không có điện nên Mirko phải mua một ngọn đèn. Mirko muốn chọn một vị trí để từ đó có thể nhìn thấy toàn bộ nền hang động.

Tưởng tượng rằng nền hang động là một đường gấp khúc trong hệ tọa độ gồm ~N~ đỉnh ~t_{1}~, ~t_{2}~,..., ~t_{N}~ . Nền hang động luôn chạy từ trái sang phải, nghĩa là với mọi ~i = 1, 2, ..., N-1~ tọa độ ~x~ của ~t_{i}~ luôn bé hơn tọa độ ~x~ của ~t_{i+1}~ .

Ví dụ: (một lời giải cho ví dụ ~3~)

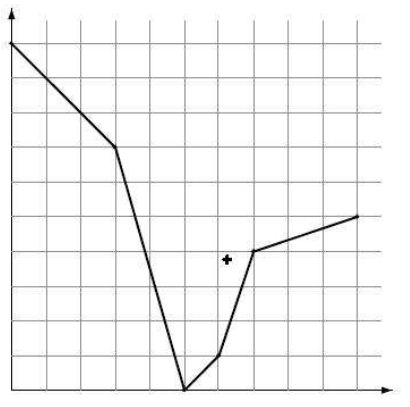
Ngọn đèn phải đặt ở một điểm nào đó "phía trên" nền hang động sao cho chiếu sáng được toàn bộ nền hang động. Chính xác hơn, tọa độ x của ngọn đèn phải được đặt giữa tọa độ ~x~ của điểm đầu và điểm cuối của hang động, và tọa độ ~y~ của ngọn đèn phải lớn hơn hoặc bằng tọa độ y của điểm nằm trên nền hang động ở cùng tọa độ ~x~.

Ngọn đèn chiếu sáng toàn bộ hang động nếu với mọi điểm thuộc nền hang động, đoạn thẳng nối điểm đó và ngọn đèn không cắt đường gấp khúc thể hiện nền hang động. Tuy nhiên, đoạn thẳng và đường gấp khúc có thể giao nhau tại các đỉnh hoặc dọc theo một đoạn thẳng thuộc đường gấp khúc.

Yêu cầu: hãy giúp Mirko xác định độ cao nhỏ nhất có thể đặt ngọn đèn để chiếu sáng toàn bộ nền hang động. Biết rằng kết quả không vượt quá ~10^6~.

Input

• Dòng đầu tiên chứa số nguyên ~N (2 \leq N \leq 5000)~ là số đỉnh của nền hang động.
• Dòng thứ ~i~ trong ~N~ dòng tiếp theo chứa 2 số nguyên ~X_{i}~, ~Y_{i}~ ~(0 \leq X_{i}, Y_{i} \leq 100,000)~, là tọa độ đỉnh thứ ~i~ của nền hang động. Các giá trị ~X_{i}~ có thứ tự tăng dần.

Output

In ra đáp án làm tròn đến chữ số thập phân thứ ~2~.

Sample Input 1

6
0 0
10 0
11 1
15 1
16 0
25 0

Sample Output 1

3.00

Sample Input 2

6
1 1
4 2
5 0
9 2
12 3
16 4

Sample Output 2

2.00

Sample Input 3

6
0 10
3 7
5 0
6 1
7 4
10 5

Sample Output 3

3.75