Mirko và Slavko chơi trò các con thú đồ chơi. Đầu tiên, Mirko và Slavko chọn một trong ~3~ bàn cờ như hình dưới đây. Mỗi bàn cờ bao gồm các ô (dưới dạng hình tròn trong hình vẽ) sắp xếp trên một lưới ~1~, ~2~ hoặc ~3~ chiều.

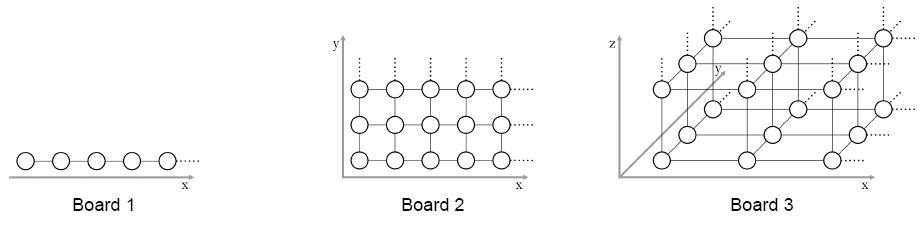
Sau đó Mirko sẽ đặt ~N~ con thú đồ chơi lên các ô.

Khoảng cách giữa ~2~ ô là số bước đi nhỏ nhất để một con thú đi từ ô này đến ô kia. Trong mỗi bước đi. con thú có thể bước đến ~1~ trong ~4~ ô kề với nó (nối với nhau bằng đoạn thẳng trong hình vẽ).

Hai con thú có thể nghe thấy nhau nếu khoảng cách giữa ~2~ ô chúng đứng không vượt quá ~D~. Nhiệm vụ của Slavko là tính số cặp con thú có thể nghe thấy nhau.

Input

Dòng đầu tiên chứa ~4~ số nguyên dương theo thứ tự:

• Loại bàn cờ ~B~ (~1 \leq B \leq 3~).

• Số con thú ~N~ (~1 \leq N \leq 10^5~).

• Khoảng cách lớn nhất ~D~ mà hai con thú có thể nghe thấy nhau (~1 \leq D \leq 10^8~).

• Kích thước bàn cờ ~M~ (tọa độ lớn nhất xuất hiện trong dữ liệu).

  • Khi ~B = 1~, ~M~ không vượt quá ~75000000~.
  • Khi ~B = 2~, ~M~ không vượt quá ~75000~.
  • Khi ~B = 3~, ~M~ không vượt quá ~75~.

Mỗi dòng trong số ~N~ dòng sau chứa ~B~ số nguyên cách nhau bởi khoảng trắng, cho biết các tọa độ của một con thú đồ chơi. Mỗi tọa độ sẽ thuộc phạm vi [ ~1~, ~M~ ]. Có thể có nhiều con thú nằm trên cùng ~1~ ô.

Output

• Gồm 1 số nguyên duy nhất là số lượng con thú có thể nghe thấy nhau.
• Lưu ý: sử dụng số nguyên 64-bit để tính kết quả (long long trong C/C++, int64 trong Pascal).

Sample Input 1

1 6 5 100
25
50
50
10
20
23

Sample Output 1

4

Sample Input 2

2 5 4 10
5 2
7 2
8 4
6 5
4 4

Sample Output 2

8

Sample Input 3

3 8 10 20
10 10 10
10 10 20
10 20 10
10 20 20
20 10 10
20 10 20
20 20 10
20 20 20

Sample Output 3

12