Bob muốn tô màu một cây ~N~ nút. Một nút được tô khi và chỉ khi nút cha của nó được tô và chỉ được tô từng nút một. Mỗi nút tô mất ~1~ đơn vị thời gian (thời điểm bắt đầu là ~0~).

Nếu ~F_i~ là thời điểm kết thúc tô nút ~i~ thì chi phí cho tô nút ~i~ là ~C_i\cdot F_i~ (~C_i~ cho trước).

Ví dụ, nếu tô cây sau theo thứ tự ~1~, ~3~, ~5~, ~2~, ~4~ và chi phí ~C_i~ cho từng nút là ~1~, ~2~, ~1~, ~2~ và ~4~ thì tổng chi phí là ~33~ và nó là nhỏ nhất.

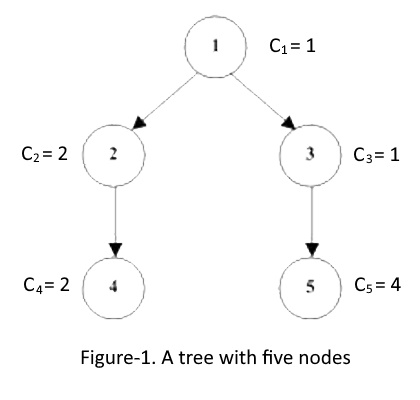
Cần tính chi phí nhỏ nhất này với một cây bất kỳ.

Input

Gồm nhiều bộ test.

Dòng đầu chứa hai số nguyên ~N~ và ~R~ (~1 \le N \le 1000~, ~1 \le R \le N~), với ~N~ là số nút và ~R~ là chỉ số của nút gốc.

Dòng thứ hai chứa ~N~ số nguyên ~C_1~, ~C_2~,.., ~C_N~ (~1 \le C_i\le 500~).

~N-1~ dòng tiếp theo mỗi dòng chứa hai số nguyên ~V_1~, ~V_2~ là cạnh nối hai nút ~V_1~ và ~V_2~, ~V_1~ là cha của ~V_2~.

Kết thúc là bộ test có ~N=R=0~ và không cần xử lý.

Output

Với mỗi bộ test, in ra chi phí nhỏ nhất cần trả.

Sample Input

5 1 
1 2 1 2 4 
1 2 
1 3 
2 4 
3 5 
0 0

Sample Output

33