Để quản lý nước cho đàn bò, FJ đã vẽ bản đồ đường ống gồm ~N~ ~\left(1 \le N \le 700\right)~ ống trong trang trại mà nối bể nước với các chuồng. FJ thấy rằng các đường ống có kích thước khác nhau và được nối một cách rất kỳ lạ. Do đó, FJ muốn tính xem lượng nước truyền qua các ống.

Hai ống nước được nối liên tiếp với nhau cho phép lượng nước không vượt quá thông lượng nhỏ nhất của hai ống.

Còn hai ống nối song song cho phép thông lượng nước là tổng thông lượng của từng ống.

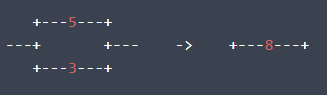
Còn một ống mà không nối với chuồng bò nào hay ống nào khác có thể bỏ đi:

Sử dụng cách thức trên, cho bản đồ đường ống, xác định lượng nước có thể truyền từ nguồn ~\left(A\right)~ cho tới chuồng ~\left(Z\right)~.

Xét ví dụ sau:

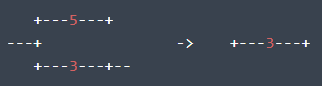
Ống ~BC~ và ~CD~ có thể gộp lại được:

Sau đó gộp ~BD~ và ~DZ~:

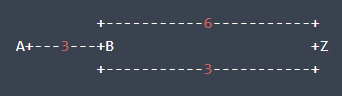
Gộp hai nhánh nối ~B~ và ~Z~:

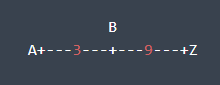
Gộp ~AB~ và ~BZ~ và thông lượng thu được là ~3~:

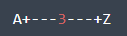
FJ cần viết một chương trình đọc vào một tập các đường ống mà mỗi đường ống được mô tả thông qua ~2~ đầu nối và tính thông lượng từ ~\left(A\right)~ tới ~\left(Z\right)~.

Mọi dữ liệu cần tính đều có thể suy luận theo các quy tắc bên trên.

Ống ~i~ nối hai nút ~a_i~ và ~b_i~ (~a_i, b_i~ là các chữ cái hoa hoặc thường - 'A-Z' hoặc 'a-z') và có thông lượng ~F_i~ ~\left(1 \leq F_i \leq 1000\right)~. Tên nút phân biệt chữ cái hoa và thường ('A' ~\ne~ 'a').

Input

• Dòng ~1~: Số nguyên ~N~
• Dòng ~2~.. ~N + 1~: Dòng ~i+1~ mô tả ống ~i~ qua hai chữ cái và một số nguyên, cách nhau bởi ~1~ dấu trống: ~a_i, b_i~ và ~F_i~

Output

• Lượng nước lớn nhất có thể truyền từ nguồn ~\left(A\right)~ tới chuồng ~\left(Z\right)~.

Sample Input

5
A B 3
B C 3
C D 5
D Z 4
B Z 6

Sample Output

3