Cho 1 hàng rào gồm ~n~ tấm ván xếp cạnh nhau, tấm ván thứ i có độ cao ~a_i~. Một decal trang trí có dạng 1 dãy các miếng dán dài ~m~, miếng thứ ~i~ có độ cao ~b_i~.

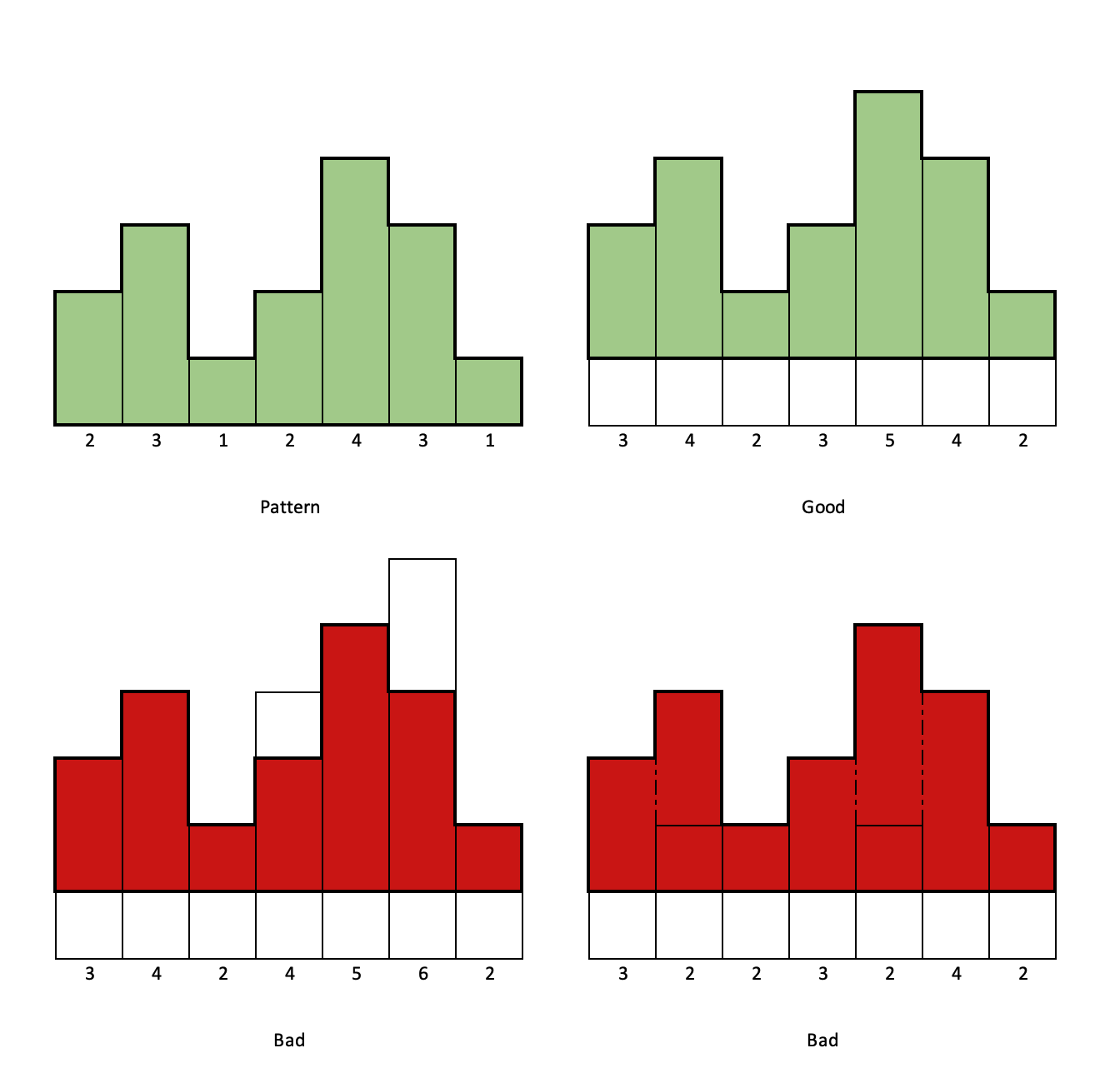
Một decal được dán hợp lệ trên 1 đoạn liên tiếp các tấm ván nếu: - Mọi ô của decal đều phủ lên ~1~ ô của tấm ván. - Với mỗi ô không được phủ bởi decal, ô bên dưới nó cũng không được phủ.

Đếm số cách hợp lệ để dán ~\geq 1~ decal lên hàng rào, sao cho không có ~2~ miếng dán nào đè lên nhau. Đáp án in ra mod ~10^9+7~.

Input

Dòng đầu tiên chứa 2 số ~n, m~ (~n, m \leq 250,000~) - độ dài của hàng rào và độ dài của miếng dán. Dòng thứ 2 chứa ~n~ số ~a_i~ (~a_i \leq 1,000,000~) - chiều cao của các đoạn hàng rào. Dòng cuối cùng chứa ~m~ số ~b_i~ (~b_i \leq 1,000,000~) - chiều cao của các đoạn decal.

Output

Một số nguyên trên một dòng duy nhất - đáp án của bài toán.

Sample Input 1

20 7
4 5 6 4 5 7 6 4 5 7 5 3 4 2 3 5 4 2 3 8 
2 3 1 2 4 3 1

Sample Output 1

3

Notes

Giải thích:

Trong test đầu tiên, decal có thể được dán ở vị trí 2, 12 hoặc là cả hai.