Chọn Đội tuyển HSGQG Quảng Trị 2024 - CONNECT
Xem dạng PDFQuốc gia Byteland xinh đẹp có ~N~ thành phố đánh số từ ~1~ đến ~N~. Có ~M~ tuyến đường một chiều nối giữa hai thành phố khác nhau, đánh số từ ~1~ đến ~M~. Có thể có nhiều hơn một tuyến đường cùng một chiều nối giữa hai thành phố.
Chính quyền Byteland chuẩn bị kế hoạch sửa chữa các tuyến đường. Tuyến đường trong thời gian sửa chữa sẽ dừng hoạt động. Một câu hỏi đặt ra cho chính quyền lúc này là: "Có thể đi từ thành phố ~A~ đến thành phố ~B~ và từ ~B~ quay lại thành phố ~A~ được hay không khi dừng hoạt động của một trong các tuyến đường của quốc gia?". Bởi sẽ có nhiều cặp thành phố cần có sự kết nối giao thông giữa chúng trong thời gian thi công các tuyến đường, bạn hãy giúp chính quyền Byteland trả lời các câu hỏi đó.
Input
Dữ liệu vào từ tệp văn bản CONNECT.INP gồm:
Dòng đầu chứa hai số nguyên ~N, M~ (~2 \leq N \leq 2000~, ~1 \leq M \leq 10^5~);
~M~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~u, v~ (~1 \leq u, v \leq N~) mô tả một tuyến đường một chiều nối từ thành phố ~u~ đến thành phố ~v~;
Dòng tiếp theo chứa số nguyên ~Q~ (~0 \leq Q \leq 10^5~):
Nếu ~Q \neq 0~ thì ~Q~ dòng tiếp theo mỗi dòng chứa hai số nguyên ~A, B~ (~1 \leq A, B \leq N~) mô tả một câu hỏi;
Nếu ~Q = 0~ thì không chứa gì thêm, khi đó bạn sẽ trả lời tất cả các câu hỏi tương ứng với các cặp có thứ tự: ~(1,1)~; ~(1,2)~; ~(1,3)~; ...; ~(1,N)~; ~(2,2)~; ~(2,3)~; ...; ~(N,N)~.
Các số trên một dòng cách nhau đúng một dấu cách.
Output
Kết quả ghi ra tệp văn bản CONNECT.OUT:
Với mỗi câu hỏi tương ứng với một cặp thành phố ~A, B~ bạn trả lời theo một trong các giá trị sau:
~0~: Nếu không dừng hoạt động tuyến đường nào mà vẫn không có đường đi cho ít nhất một trong hai hướng (từ ~A~ đến ~B~ hoặc từ ~B~ đến ~A~);
~M + 1~: Nếu dừng hoạt động của bất kỳ tuyến đường nào thì cũng có đường đi từ ~A~ đến ~B~ và từ ~B~ quay lại ~A~;
~E~: Là một số trong khoảng từ ~1~ đến ~M~ là số hiệu tuyến đường mà khi dừng hoạt động tuyến đường đó thì sẽ không có đường đi cho ít nhất một trong hai hướng. Nếu có nhiều tuyến đường như vậy thì ghi ra tuyến đường có số hiệu nhỏ nhất.
Để ghi ra các giá trị này bạn thực hiện theo yêu cầu sau:
Gọi ~r_1, r_2, \dots, r_k~ là các giá trị trả lời cho ~Q~ câu hỏi (~K = Q~) trong trường hợp ~Q \neq 0~, nếu ~Q = 0~ thì ~K = \frac{N \times (N+1)}{2}~;
Kết quả ghi ra tệp gồm một dòng ghi một số là phần dư của số nguyên ~P~ khi chia cho ~10^9 + 7~ với: $$P = r_1 \times B^{K-1} + r_2 \times B^{K-2} + r_3 \times B^{K-3} + \dots + r_K \times B^0$$ trong đó ~B = 2 \times 10^5~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~15\%~ | ~N \leq 200~, ~M \leq 1000~, ~Q \leq 500~ và ~Q \neq 0~ |
| 2 | ~15\%~ | ~N \leq 2000~, ~M \leq 10^5~, ~Q \leq 10^5~ và kết quả trả lời các câu hỏi chỉ một trong hai giá trị: ~0~ hoặc ~M+1~ |
| 3 | ~20\%~ | ~N \leq 500~, ~M \leq 8000~, ~Q \leq 10^5~ |
| 4 | ~25\%~ | ~N \leq 2000~, ~M \leq 10^5~, ~Q \leq 10^4~, ~Q \neq 0~ |
| 5 | ~25\%~ | Không có ràng buộc gì thêm |
Sample Input 1
6 11
1 4
4 3
3 5
5 1
1 3
3 6
5 6
6 2
4 2
5 1
3 5
0
Sample Output 1
575589257
Sample Input 2
8 17
5 2
6 5
4 6
4 8
4 3
3 1
2 7
7 4
5 4
8 7
8 3
3 6
6 1
2 4
1 5
1 5
5 2
4
4 6
8 1
5 2
6 7
Sample Output 2
995598902
Notes
Ở test ví dụ thứ nhất:
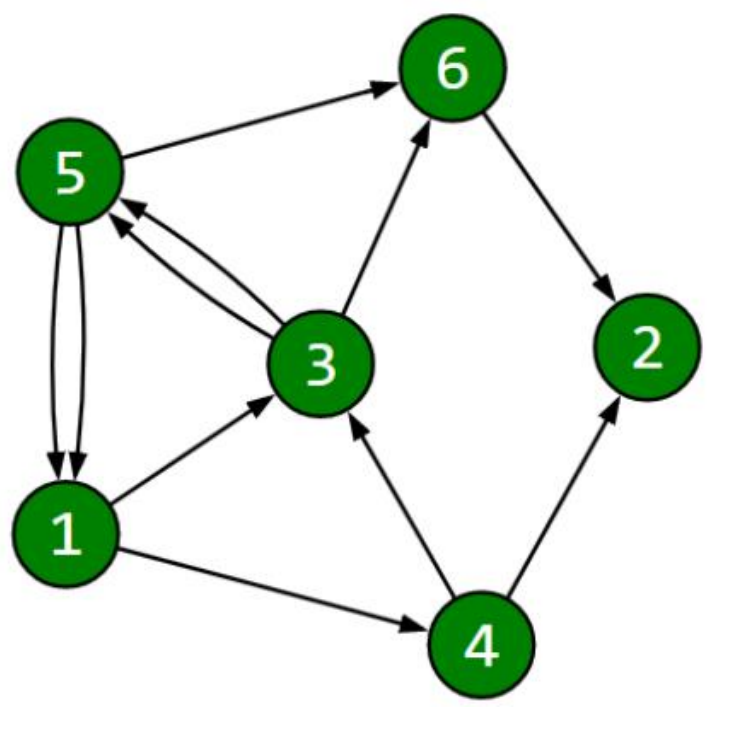
Câu hỏi ~(1, 6)~: Không có đường đi từ 6 về 1 trong khi không dừng hoạt động tuyến đường nào.
Câu hỏi ~(1, 3)~: Dừng hoạt động bất kỳ tuyến đường nào thì cũng có đường đi theo cả hai hướng giữa ~1~ và ~3~.
Câu hỏi ~(4, 5)~: Khi dừng hoạt động tuyến đường từ ~1~ đến ~4~ (số hiệu ~1~) thì sẽ không có đường đi từ ~5~ đến ~4~.
Dãy kết quả tương ứng: 12 0 12 1 12 0 12 0 0 0 0 12 1 12 0 12 1 0 12 0 12.
Ở test ví dụ thứ hai:
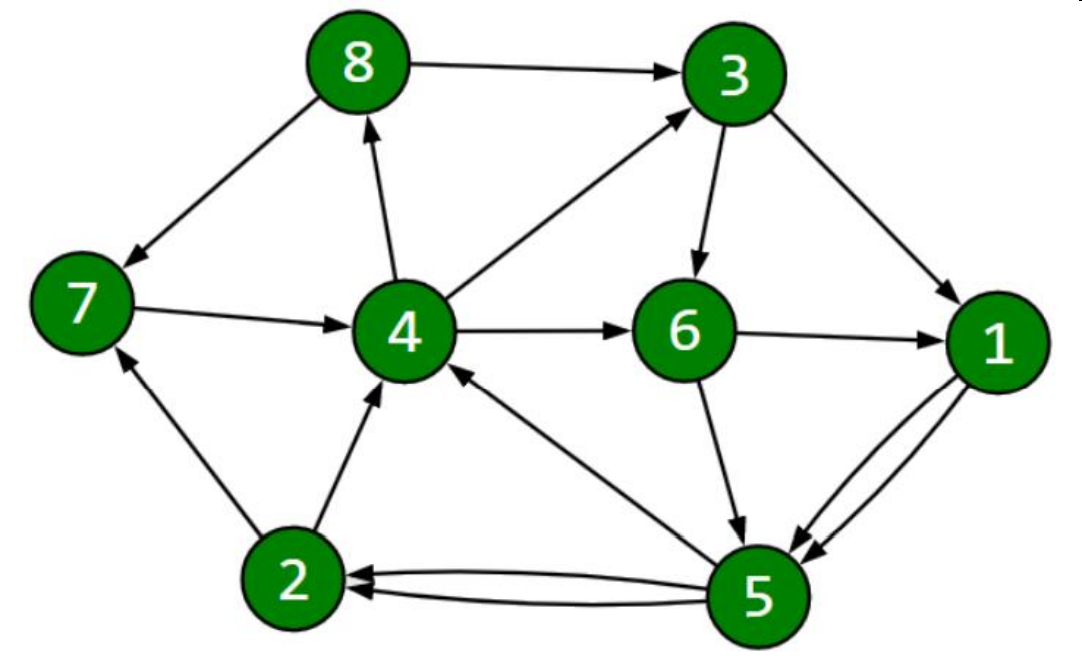
Câu hỏi ~(8, 1)~: Nếu dừng hoạt động tuyến đường từ ~4~ đến ~8~ thì sẽ không có đường đi từ ~1~ đến ~8~.
Câu hỏi ~(6, 7)~: Nếu dừng hoạt động tuyến đường từ ~7~ đến ~4~ thì sẽ không có đường đi từ ~7~ đến ~6~.
Dãy kết quả tương ứng: 18 4 18 8.

Bình luận