Hướng dẫn giải của Chọn Đội tuyển HSGQG Huế 2024 - Khám phá mê cung
Nộp một lời giải chính thức trước khi tự giải là một hành động có thể bị ban.
Subtask 1:
~n, q \le 100~ và ~k \le 100~.
Với mỗi truy vấn, mô phỏng lại chính xác cách di chuyển được miêu tả trong đề bài.
Độ phức tạp mỗi truy vấn: ~O(k)~ hoặc ~O(n + k)~ tùy cách cài đặt.
Subtask 2:
~k \le 10^5~.
Khi chúng ta mô phỏng lại cách di chuyển như ở Subtask 1 để tính toán kết quả cho ~k~, ta xây dựng trạng thái của mê cung khi ta di chuyển ~1, 2, \ldots, k~ bước. Vì vậy, khi áp dụng thuật toán ở Subtask 1 cho giá trị ~k~ nào đó, ta có thể trả lời các truy vấn có giá trị ~1, 2, \ldots, k~.
Áp dụng Subtask 1 cho giá trị ~k = 10^5~ và lưu tất cả các đáp án trong khi mô phỏng. Độ phức tạp ~O(n + k)~.
Sau đó, ta dễ dàng trả lời từng truy vấn trong ~O(1)~.
Subtask 3:
~n, q \le 1000~ và tồn tại một đường hầm nối hai phòng ~i~ và ~i + 1~ với mọi ~1 \le i \lt n~
Ta chia đường đi thành nhiều đoạn nhỏ, mỗi đoạn là một chu trình xuất phát từ đỉnh ~1~ và kết thúc tại đỉnh ~1~:
Nếu ở mọi phòng ~i~, đèn laser chỉ đến phòng ~i - 1~ (với ~2 \le i \le n~) thì chu trình có dạng là ~1 \to 2 \to \ldots n - 1 \to n \to n - 1 \to \ldots \to 2 \to 1~.
Nếu tồn tại một phòng ~i~ có đèn laser chỉ đến phòng ~i + 1~ và mọi phòng ~j~ với ~2 \le j < i~ đều có đèn laser chỉ đến phòng ~i - 1~ thì chu trình có dạng là ~1 \to 2 \to \ldots i - 1 \to i \to i - 1 \to \ldots \to 2 \to 1~. Sau chu trình này, chỉ duy nhất phòng ~i~ có laser đổi chiều từ hướng ~i + 1~ thành ~i - 1~.
Xét đồ thị có các đỉnh ~v_1, v_2, \ldots v_m~ sao cho các đèn laser tại phòng ~v_i~ đều chỉ tới phòng ~v_i + 1~ (~v_i > 1~, ~1 \le i \le m~), các chu trình lần lượt là:
Chu trình thứ ~1~: ~1 \to 2 \to \ldots v_1 - 1 \to v_1 \to v_1 - 1 \to \ldots \to 2 \to 1~.
Chu trình thứ ~2~: ~1 \to 2 \to \ldots v_2 - 1 \to v_2 \to v_2 - 1 \to \ldots \to 2 \to 1~.
~\ldots~
Chu trình thứ ~m~: ~1 \to 2 \to \ldots v_m - 1 \to v_m \to v_m - 1 \to \ldots \to 2 \to 1~.
Mọi chu trình sau đó: ~1 \to 2 \to \ldots \to n - 1 \to n \to n - 1 \to \ldots \to 2 \to 1~.
Dễ thấy, các chu trình có độ dài không quá ~2 \times n - 1~. Ta có thể dễ dàng xây dựng ~m~ chu trình đầu tiên.
Với mỗi truy vấn, nếu kết quả nằm trong ~m~ chu trình đầu tiên, ta có thể trả lời từ ~m~ chu trình đã xây dựng. Ngược lại, nếu truy vấn không nằm trong ~m~ chu trình đầu tiên, ta sử dụng việc các chu trình sau ~m~ chu trình đầu tiên đều có dạng ~1 \to 2 \to \ldots n - 1 \to n \to n - 1 \to \ldots \to 2 \to 1~ để trả lời.
Độ phức tạp: ~O(n^2 + q)~.
Subtask 4:
~n, q \le 1000~.
Ta chia đường đi thành nhiều đoạn nhỏ, mỗi đoạn là một chu trình xuất phát từ đỉnh ~1~, kết thúc tại đỉnh ~1~ và đi qua MỌI đỉnh kề với đỉnh ~1~.
Các chu trình này sẽ có độ dài không quá ~2 \times n - 1~ do mỗi chu trình sẽ tương ứng với đường đi Euler trên một phần của cây.
Các đỉnh xuất hiện trong chu trình thứ ~i~ thì xuất hiện ở chu trình ~i + 1~.
Gọi đỉnh ~p_i~ là đỉnh tổ tiên trực tiếp của đỉnh ~i~. Nếu đỉnh ~p_i~ xuất hiện trong chu trình thứ ~j~ thì đỉnh ~i~ xuất hiện trong chu trình ~j~ hoặc ~j + 1~.
Từ các nhận xét trên, các chu trình sau chu trình thứ ~n~ sẽ lặp lại. Ta chỉ cần xây dựng ~n + 1~ chu trình đầu tiên và trả lời các truy vấn như Subtask 3.
Subtask 5:
không có ràng buộc gì thêm.
Ta chia đường đi thành các chu trình như Subtask 4. Vì các chu trình tương ứng với đường đi Euler trên một phần của cây nên các chu trình là một dãy con của đường đi Euler trên toàn bộ cây.
Ví dụ:
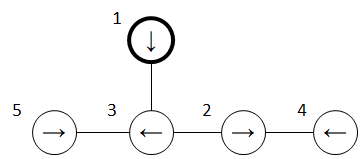
| Euler tour | 1 | 3 | 2 | 4 | 2 | 3 | 5 | 3 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| Chu trình 1 | 1 | 3 | 1 | ||||||
| Chu trình 2 | 1 | 3 | 2 | 3 | 5 | 3 | 1 | ||
| Chu trình 3 | 1 | 3 | 2 | 4 | 2 | 3 | 5 | 3 | 1 |
| Chu trình 4 | 1 | 3 | 2 | 4 | 2 | 3 | 5 | 3 | 1 |
Ở bảng trên, ta thấy có đỉnh ~3~ xuất hiện ba lần ở vị trí ~2~, ~6~ và ~8~.
Đỉnh ~3~ nằm ở vị trí ~2~ với ý nghĩa là lần đầu tiên đỉnh ~3~ được thăm.
Đỉnh ~3~ nằm ở vị trí ~6~ với ý nghĩa là lần quay lại đỉnh ~3~ từ đỉnh ~2~.
Đỉnh ~3~ nằm ở vị trí ~8~ với ý nghĩa là lần quay lại đỉnh ~3~ từ đỉnh ~5~.
Từ đó, ta cần xác định lần đầu tiên một đỉnh xuất hiện trong chu trình là khi nào để biết thứ tự thêm các đỉnh vào đường đi Euler. Điều này có thể thực hiện bằng quy hoạch động:
Gọi ~f[i]~ là lần đầu tiên đỉnh ~i~ xuất hiện trong chu trình. Cơ sở: ~f[1] = 1~.
Xét đỉnh ~u~ cố định.
Gọi ~c_1, c_2, \ldots c_d~ là danh sách các đỉnh kề đỉnh ~u~.
Gọi ~p~ là vị trí đỉnh tổ tiên của ~u~ trong danh sách ~c~ (~c_p~ là tổ tiên của ~u~).
Khi đỉnh ~u~ lần đầu tiên xuất hiện trong chu trình, đường đi sẽ tiếp tục đi qua cây con gốc ~c_2, c_3, \ldots c_{p - 2}, c_{p - 1}~ sau đó rời khỏi cây con gốc ~u~ và quay lại đỉnh ~c_p~. Suy ra, ~f[c_i] = f[u]~ với ~2 \le i \lt p~.
Các đỉnh còn lại sẽ có lần đầu xuất hiện ở chu trình sau: ~f[c_i] = f[u] + 1~ với ~i < 2~ hoặc ~p \lt i \le d~.
Từ đây, ta có thể xây dựng các chu trình từ chu trình trước đó bằng cách thêm các đỉnh vào chu trình. Để thêm các đỉnh vào chu trình và đồng thời truy vấn tìm đỉnh thứ ~i~ trong chu trình đó, ta sử dụng cấu trúc dữ liệu Segment Tree để quản lí các chu trình.
Phần còn lại của bài toán, sắp xếp các truy vấn theo thứ tự tăng dần và sử dụng hai con trỏ để xử lí các truy vấn theo quá trình xây dựng các chu trình.
Độ phức tạp: ~O(n \log n + q \log q)~.
#include <bits/stdc++.h> using namespace std; template<typename T> struct SegmenTree { vector<T> tree; int n; function<T(T, T)> merge; T neutral; SegmenTree(int n, function<T(T, T)> merge, T neutral) : n(n), merge(merge), neutral(neutral), tree(4 * n, neutral) {} SegmenTree(int n) : SegmenTree(n, [](T a, T b) { return a + b; }, 0) {} void ins(int p, T val) { assert(0 <= p && p < n); _ins(0, 0, n, p, val); } void _ins(int k, int l, int r, int p, T val) { if (r - l == 1) { tree[k] = val; return; } int m = (l + r) >> 1; if (p < m) { _ins(2 * k + 1, l, m, p, val); } else { _ins(2 * k + 2, m, r, p, val); } tree[k] = merge(tree[2 * k + 1], tree[2 * k + 2]); } int _find(int k, int l, int r, T s) { if (r - l == 1) { return r; } int m = (l + r) >> 1; if (tree[2 * k + 1] >= s) { return _find(2 * k + 1, l, m, s); } else { return _find(2 * k + 2, m, r, s - tree[2 * k + 1]); } } // find the first index i such that sum[0, i) >= s int find(T s) { if (s == 0) return 0; return _find(0, 0, n, s); } T total() { return tree[0]; } }; int32_t main(){ ios_base::sync_with_stdio(false); cin.tie(0); #define Task "MAZE" freopen(Task".INP", "r", stdin); freopen(Task".OUT", "w", stdout); int n, q; cin >> n >> q; vector<vector<int>> adj(n); for (int i = 0; i < n; ++i) { int d; cin >> d; adj[i].resize(d); cin >> adj[i][d - 1]; adj[i][d - 1]--; for (int j = 0; j < d - 1; ++j) { cin >> adj[i][j]; adj[i][j]--; } } vector<long long> queries(q); for (int i = 0; i < q; ++i) { cin >> queries[i]; } vector<int> euler_tour; vector<vector<int>> circuits(n); vector<int> first_circuit(n, 0); int max_circuit = 0; function<void(int, int)> dfs = [&](int u, int p) { if (p != -1) { circuits[first_circuit[u]].push_back(euler_tour.size()); euler_tour.push_back(u); } int pid = adj[u].size(); for (int i = 0; i < (int)adj[u].size(); ++i) { if (adj[u][i] == p) { pid = i; break; } } for (int i = pid + 1; i < (int)adj[u].size(); ++i) { int v = adj[u][i]; first_circuit[v] = first_circuit[u] + 1; max_circuit = max(max_circuit, first_circuit[v]); dfs(v, u); circuits[first_circuit[v]].push_back(euler_tour.size()); euler_tour.push_back(u); } for (int i = 0; i < pid; ++i) { int v = adj[u][i]; first_circuit[v] = first_circuit[u]; max_circuit = max(max_circuit, first_circuit[v]); dfs(v, u); circuits[first_circuit[v]].push_back(euler_tour.size()); euler_tour.push_back(u); } }; first_circuit[0] = 0; dfs(0, -1); vector<int> query_idx(q); iota(query_idx.begin(), query_idx.end(), 0); sort(query_idx.begin(), query_idx.end(), [&](int i, int j) { return queries[i] < queries[j]; }); SegmenTree<long long> st(euler_tour.size()); int cur_circuit = 0; long long sum = 0; vector<int> ans(q); for (int i = 0; i < q; ++i) { long long query = queries[query_idx[i]]; while (cur_circuit <= max_circuit && sum < query) { for (int j = 0; j < (int)circuits[cur_circuit].size(); ++j) { st.ins(circuits[cur_circuit][j], 1); } sum += st.total(); cur_circuit++; } if (sum >= query) { int idx = st.find(query - (sum - st.total())); ans[query_idx[i]] = euler_tour[idx - 1] + 1; } else { int idx = st.find((query - sum) % st.total()); if (idx == 0) { idx = st.total(); } ans[query_idx[i]] = euler_tour[idx - 1] + 1; } } for (int i = 0; i < q; ++i) { cout << ans[i] << '\n'; } return 0; }
Bình luận