Hướng dẫn giải của Bedao SUBSEQUENCE Hay Không? Hay Hay
Nộp một lời giải chính thức trước khi tự giải là một hành động có thể bị ban.
Author:
Ý tưởng:
Xét mảng ~a[1…n]~ được xếp theo thứ tự không giảm ~(a_1 \le a_2 \le … \le a_n)~, dễ thấy có ~2^{i-1}~ subsequence nhận ~a_i~ làm phần tử lớn nhất.
Vậy bài toán tương đương dựng mảng ~a[1…n]~ sao cho :
~a_i \le a_{i+1}~
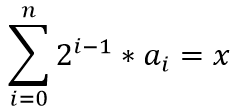
Vì mọi số ~a_i~ có dạng ~2^k~ đều thỏa mãn yêu cầu của đề bài, ý tưởng ở đây là ta sẽ sử dụng chúng để khôi phục lại biểu diễn nhị phân của số ~x~.
Xét biểu diễn nhị phân của số ~x~, gọi một bit là bật nếu như bit đó bằng ~1~, ta dựng mảng ~a[1…n]~ sao cho ~n~ chính bằng số bit bật trong biểu diễn nhị phân của ~x~ và mỗi phần tử ~a_i~ sẽ tương đương với một bit bật.
Gọi ~b_i~ là vị trí của bit thứ ~i~ được bật từ bên phải sang, khi biết biểu diễn của số ~x~ trong hệ nhị phân ta có thể tính giá trị của ~x~ trong hệ thập phân bằng công thức sau :

Vậy ta sẽ dựng mảng ~a[1…n]~ sao cho:
- ~2^{i-1} \times a_i = 2^{b_i} ↔ a_i = \frac{2^{b_i}}{2^{i-1}}=2^{b_i - (i-1)}~
Dễ thấy ~b_i \ge (i-1)~ và ~b_{i+1}-b_i \ge 1⟶ a_i \ge a_{i+1}~ nên mảng ~a[1…n]~ luôn thỏa mãn đề bài
Code mẫu
#include <bits/stdc++.h> using namespace std; #define fo(i, a, b) for(int i = a; i <= b; i++) #define _fo(i, a, b) for(int i = a; i >= b; i--) #define foa(i, a) for (auto &i : a) #define sz(a) ((int) a.size()) #define all(a) begin(a), end(a) #define fi first #define se second #define pb(x) push_back(x) #define mk(x, y) make_pair(x, y) typedef long long ll; typedef pair<ll, ll> pll; typedef vector<ll> vl; typedef pair<int, int> pii; typedef vector<int> vi; const int MAX = 2e5+5; const int LOG = 20; const int MOD = 998244353; const ll INF = 1e15+5; ll add(ll a, ll b) { return (a+b) % MOD; } ll sub(ll a, ll b) { return (a-b+MOD) % MOD; } ll mul(ll a, ll b) { return (a*b) % MOD; } vector<ll> ans; void solve(ll val) { ll contribution = 1; while(val > 0) { ll temp = val&(-val); ans.pb(temp/contribution); contribution *= 2; val -= temp; } cout << sz(ans) << "\n"; foa(elem, ans) cout << elem << " "; cout << "\n"; ans.clear(); } int main() { ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0); int t; cin >> t; while(t--) { ll x; cin >> x; solve(x); } }
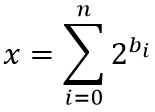
Bình luận