Hướng dẫn giải của Bedao PERMSORT Hay Không? Hay Hay
Nộp một lời giải chính thức trước khi tự giải là một hành động có thể bị ban.
Nguồn bài: DMOPC '21 Contest 3 P4
Ý tưởng
Vì cần tìm hoán vị có thứ tự từ điển nhỏ nhất nên ta có thể dùng giải thuật tham lam: Với mỗi vị trí lần lượt từ ~1~ đến ~N~, tìm phần tử nhỏ nhất có thể đưa về vị trí đó.
Để dễ hình dung thì ta sẽ nối phần tử tại vị trí ~i~ với phần tử tại vị trí ~j~ bằng một cạnh có hướng (từ ~i~ đến ~j~) nếu sau khi sắp xếp, phần tử tại ~i~ di chuyển đến vị trí ~j~. Minh hoạ với ví dụ thứ hai:
Dễ thấy mỗi thao tác sắp xếp dãy con tương đương với một chu trình có hướng. Ta sẽ tham lam xây dựng dần các cạnh này, tạo thành chuỗi các đỉnh như sau: Với mỗi vị trí từ ~1~ đến ~N~, nối phần tử có giá trị nhỏ nhất có thể nổi với vị trí đó. Điều kiện để nối vị trí ~i~ với vị trí ~j~ là ~i~ chưa nối với vị trị nào khác và sau khi nối chuỗi mới có kích thước không vượt quá ~K~. Lưu ý rằng các cạnh có thể nối hai chuỗi khác nhau hoặc nối hai phần tử cùng một chuỗi để hoàn thành chu trình. Cạnh cũng có thể nối một phần tử với chính nó (tức vị trí của phần tử đó không đổi).
Minh hoạ từng bước với ví dụ thứ hai:
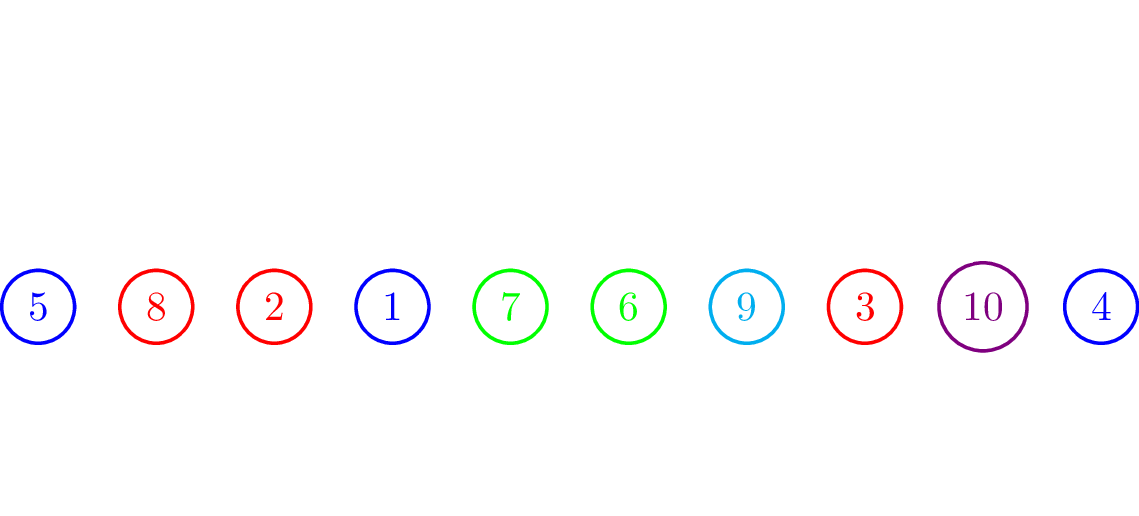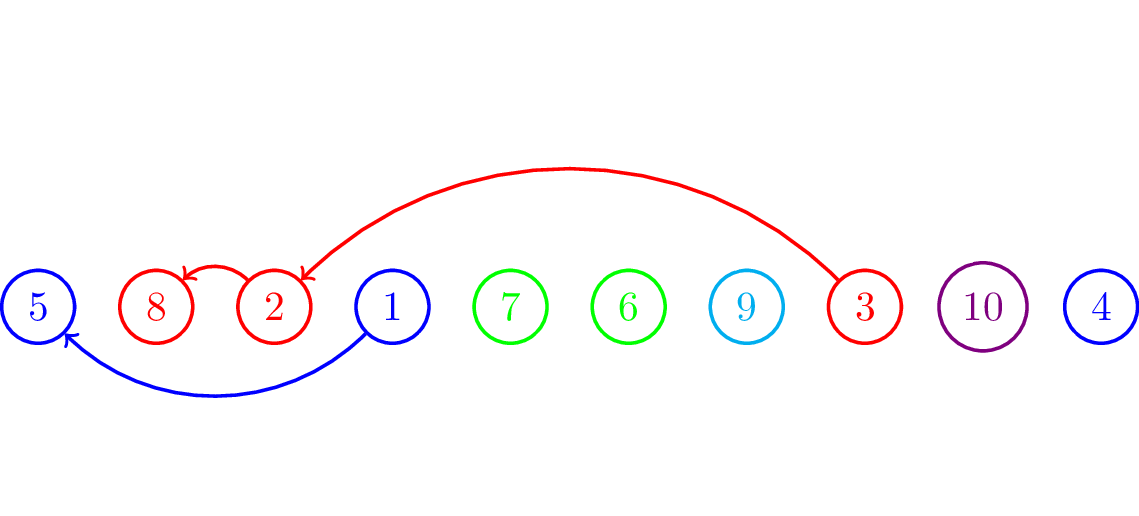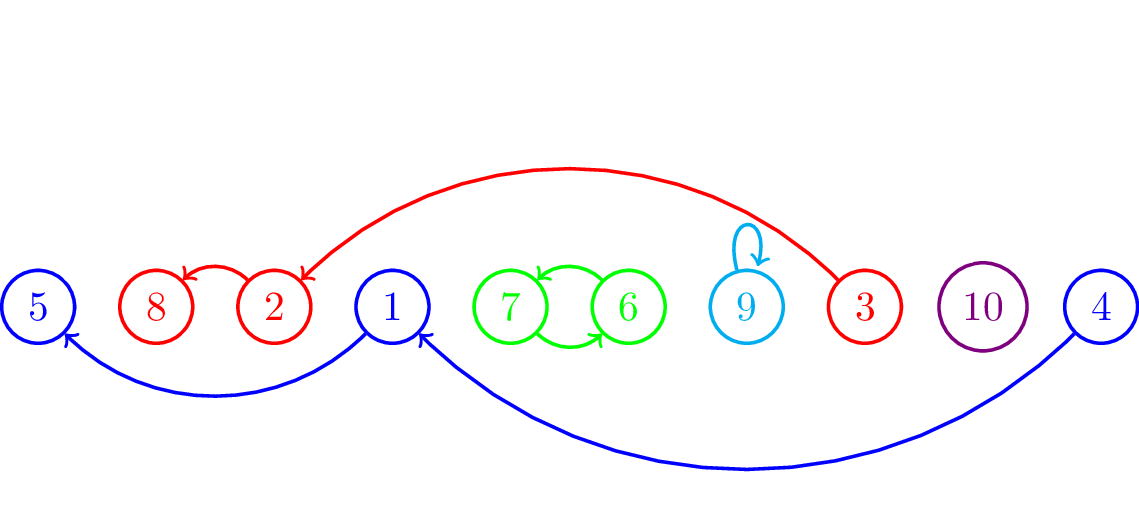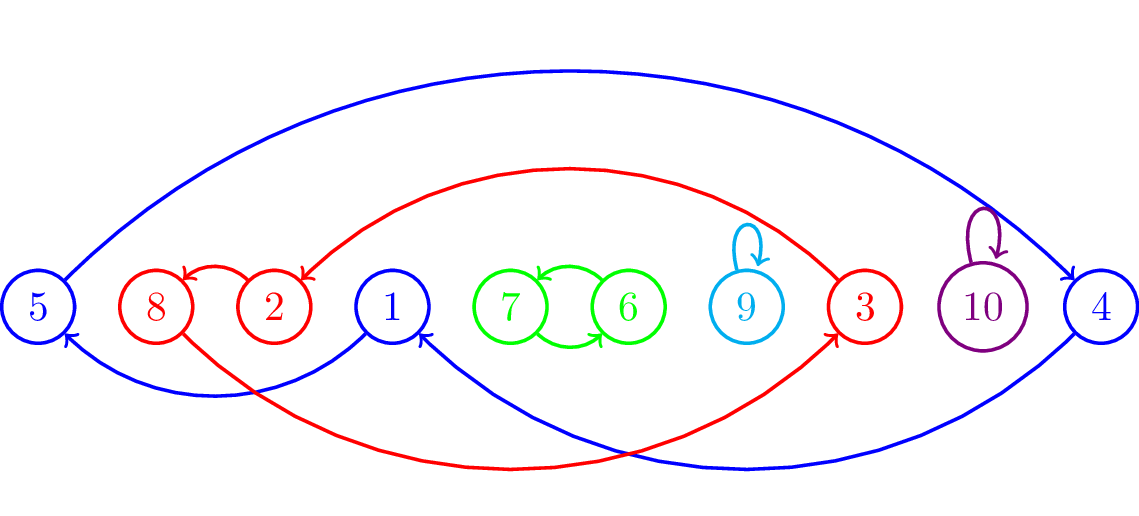
Để lưu thông tin mỗi chuỗi thì ta có thể dùng Disjoint Set Union (DSU). Sau khi xây dựng tất cả các chu trình thì ta tiến hành việc sắp xếp.
Ta có thể chứng minh được sau khi sắp xếp các phần tử sẽ về đúng vị trí như biểu diễn cạnh bằng nhận xét: Trong cùng một chu trình, khi duyệt các vị trí tăng dần thì các giá trị được gán vào các vị trí đấy cũng tăng dần.
Ngoài ra còn một cách cài đặt khác không dùng DSU, đó là swap các phần tử ngay ở bước tìm (xem code để hiểu thêm).
Subtask 1
Ở bước tìm phần tử có giá trị nhỏ nhất ta chỉ cần duyệt qua tất cả các phần tử và thử nối.
Độ phức tạp: ~O(N^2)~
Subtask 2
Dùng Segment Tree để lưu kích thước của chuỗi ứng với mỗi giá trị. Để tìm giá trị nhỏ nhất nối được ta chặt nhị phân trên Segment Tree (Walking on Segment Tree).
Độ phức tạp: ~O(N \log N)~
Cài đặt bằng DSU
Subtask 1:
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 5; int n, k, a[N], pos[N], par[N], ans[N]; vector<int> order, group[N]; bool mark[N]; int root(int v) { return (par[v] < 0) ? v : (par[v] = root(par[v])); } void join(int x, int y) { if ((x = root(x)) == (y = root(y))) return; if (par[x] > par[y]) swap(x, y); par[x] += par[y]; par[y] = x; } int main() { ios::sync_with_stdio(false); cin.tie(0); cin >> n >> k; for (int i = 1; i <= n; ++i) { cin >> a[i]; par[i] = -1; order.emplace_back(i); } sort(order.begin(), order.end(), [&](const int &x, const int &y) { return a[x] < a[y]; }); for (int i = 1; i <= n; ++i) { int ind = -1; for (int x : order) { if (mark[x]) continue; if (root(x) == root(i) || -par[root(x)] - par[root(i)] <= k) { ind = x; break; } } assert(ind != -1); join(i, ind); pos[ind] = i; mark[ind] = true; } for (int i = 1; i <= n; ++i) { group[root(i)].emplace_back(i); } for (int i = 1; i <= n; ++i) { if (par[i] > 0) continue; vector<int> val; for (int x : group[i]) { val.emplace_back(a[x]); } sort(group[i].begin(), group[i].end()); sort(val.begin(), val.end()); for (int j = 0; j < (int)group[i].size(); ++j) { ans[group[i][j]] = val[j]; } } for (int i = 1; i <= n; ++i) { assert(ans[pos[i]] == a[i]); } for (int i = 1; i <= n; ++i) { cout << ans[i] << " \n"[i == n]; } return 0; }
Subtask 2:
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 5; int n, k, p[N], q[N], pos[N], par[N], head[N], ans[N], st[N << 2]; vector<int> group[N]; void update(int id, int l, int r, int pos, int v) { if (l == r) { st[id] = v; return; } int mid = (l + r) >> 1; if (pos <= mid) { update(id << 1, l, mid, pos, v); } else { update(id << 1 | 1, mid + 1, r, pos, v); } st[id] = min(st[id << 1], st[id << 1 | 1]); } int find(int id, int l, int r, int v) { if (st[id] > v) return -1; if (l == r) return l; int mid = (l + r) >> 1; if (st[id << 1] <= v) { return find(id << 1, l, mid, v); } else { return find(id << 1 | 1, mid + 1, r, v); } } int root(int v) { return (par[v] < 0) ? v : (par[v] = root(par[v])); } void join(int x, int y, int h) { if ((x = root(x)) == (y = root(y))) return; if (par[x] > par[y]) swap(x, y); head[x] = h; par[x] += par[y]; par[y] = x; } int main() { ios::sync_with_stdio(false); cin.tie(0); cin >> n >> k; for (int i = 1; i <= n; ++i) { cin >> p[i]; q[p[i]] = i; par[i] = -1; head[i] = i; update(1, 1, n, i, 1); } for (int i = 1; i <= n; ++i) { int val = find(1, 1, n, k + par[root(i)]); if (val != -1 && val < p[head[root(i)]]) { int ind = q[val]; pos[ind] = i; update(1, 1, n, val, 1e9); if (root(ind) != root(i)) { join(i, ind, head[root(i)]); update(1, 1, n, p[head[root(i)]], -par[root(i)]); } } else { int h = head[root(i)]; pos[h] = i; update(1, 1, n, p[h], 1e9); } } for (int i = 1; i <= n; ++i) { group[root(i)].emplace_back(i); } for (int i = 1; i <= n; ++i) { if (par[i] > 0) continue; vector<int> val; for (int x : group[i]) { val.emplace_back(p[x]); } sort(group[i].begin(), group[i].end()); sort(val.begin(), val.end()); for (int j = 0; j < (int)group[i].size(); ++j) { ans[group[i][j]] = val[j]; } } for (int i = 1; i <= n; ++i) { assert(ans[pos[i]] == p[i]); } for (int i = 1; i <= n; ++i) { cout << ans[i] << " \n"[i == n]; } return 0; }
Cài đặt bằng cách swap trực tiếp
Subtask 1:
#include <bits/stdc++.h> using namespace std; int main() { ios::sync_with_stdio(false); cin.tie(0); int n, k; cin >> n >> k; vector<int> p(n), cost(n, 1); for (int& x : p) cin >> x; for (int pos = 0; pos < n; ++pos) { int ok_pos = -1; for (int i = pos + 1; i < n; ++i) { if (cost[i] + cost[pos] > k) continue; if (ok_pos == -1 || p[ok_pos] > p[i]) ok_pos = i; } if (ok_pos != -1 && p[pos] > p[ok_pos]) { swap(p[pos], p[ok_pos]); cost[ok_pos] += cost[pos]; } } for (int i = 0; i < n; ++i) { cout << p[i] << " \n"[i == n - 1]; } return 0; }
Subtask 2:
#include <bits/stdc++.h> using namespace std; int main() { ios::sync_with_stdio(false); cin.tie(0); int n, k; cin >> n >> k; vector<int> p(n), q(n + 1), cost(n, 1), st(4 * n, 1); for (int i = 0; i < n; ++i) { cin >> p[i]; q[p[i]] = i; } function<void(int, int, int, int, int)> update = [&](int id, int l, int r, int pos, int v) { if (l == r) { st[id] = v; return; } int m = (l + r) / 2; if (pos <= m) { update(id * 2, l, m, pos, v); } else { update(id * 2 + 1, m + 1, r, pos, v); } st[id] = min(st[id * 2], st[id * 2 + 1]); }; function<int(int, int, int, int)> find = [&](int id, int l, int r, int v) { if (st[id] > v) return -1; if (l == r) return l; int m = (l + r) / 2; if (st[id * 2] <= v) { return find(id * 2, l, m, v); } else { return find(id * 2 + 1, m + 1, r, v); } }; for (int pos = 0; pos < n; ++pos) { int val = find(1, 1, n, k - cost[pos]); if (val != -1 && p[pos] > val) { int ok_pos = q[val]; swap(p[pos], p[ok_pos]); swap(q[p[pos]], q[p[ok_pos]]); cost[ok_pos] += cost[pos]; update(1, 1, n, p[ok_pos], cost[ok_pos]); } cost[pos] = 1e9; update(1, 1, n, p[pos], cost[pos]); } for (int i = 0; i < n; ++i) { cout << p[i] << " \n"[i == n - 1]; } return 0; }
Bình luận
Trong cái code sub1 với DSU, mình không hiểu cái chỗ:
Tại sao lại sort theo a[x] < a[y] vậy?