Cho số nguyên dương ~n~ và dãy số nguyên dương ~a_1, a_2,...a_n~, với ~\frac{i(i-1)}{2} < a_i \leq \frac{i(i+1)}{2}~.

Dãy số đó tham số hóa cho một cây với ~\frac{(n+1)(n+2)}{2}~ đỉnh, phân ra thành ~n+1~ tầng với lần lượt ~1, 2, ..., n+1~ đỉnh ở mỗi tầng tương ứng, như trong hình sau:

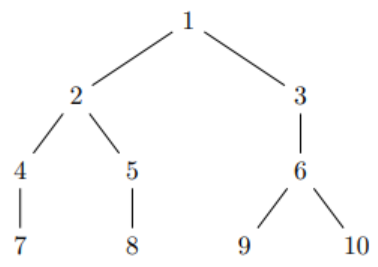
Cây được tham số hóa bởi mảng ~a = (1,2,6)~

Tầng thứ ~i~ chứa các đỉnh ~\frac{i(i-1)}{2}+1 ,..., \frac{i(i+1)}{2}~. Đỉnh ~a_i~ có 2 con, còn những đỉnh còn lại trong tầng đó, mỗi đỉnh chỉ có ~1~ con duy nhất.

Bạn phải trả lời ~q~ truy vấn ở dạng: Tổ tiên chung lớn nhất của đỉnh ~x~ và đỉnh ~y~ là đỉnh nào? Nói cách khác, đó chính là đỉnh với số hiệu lớn nhất mà cây con với gốc là đỉnh đó có chứa cả ~x~ và ~y~.

Input

Dòng đầu tiên chứa ~3~ số nguyên ~n~, ~q~ và ~t~ ~(1 \leq n,q \leq 200000, t \in \{ 0,1 \})~, lần lượt là số lượng các số trong dãy, số lượng truy vấn và một giá trị sẽ được dùng để xác định số hiệu của các đỉnh trong các truy vấn.

Dòng thứ 2 chứa dãy số gồm ~n~ số nguyên ~a_i~ ~(\frac{i(i-1)}{2} < a_i \leq \frac{i(i+1)}{2})~ tham số hóa cho cây.

Dòng thứ ~i~ trong số ~q~ dòng tiếp theo chứa 2 số nguyên ~\tilde{x}_i, \tilde{y}_i~ ~(1 \leq \tilde{x}_i, \tilde{y}_i \leq \frac{(n+1)(n+2)}{2})~ sẽ được dùng để xác định số hiệu của các đỉnh ở truy vấn này.

Đặt ~z_i~ là đáp án của truy vấn thứ ~i~, và ~z_0 = 0~. Số hiệu của ~x_i~ và ~y_i~ ở truy vấn thứ ~i~ được xác định bởi công thức:

~x_i = ( (\tilde{x}_i - 1 + t * z_{i-1} )~ ~mod~ ~\frac{(n+1)(n+2)}{2}) + 1~,

~y_i = ( (\tilde{y}_i - 1 + t * z_{i-1} )~ ~mod~ ~\frac{(n+1)(n+2)}{2}) + 1~,

với mod là phép chia số nguyên lấy dư.

Chú ý:

Nếu ~t = 0~, thì ~x_i = \tilde{x}_i ~ và ~y_i = \tilde{y}_i ~, khi đó truy vấn được nhập ngay từ input

Nếu ~t = 1~, tất cả truy vấn không được biết trước, nhưng được xác định bằng cách sử dụng đáp án của các truy vấn trước đó.

Output

In ra ~q~ dòng. Ở dòng thứ ~i~, in ra tổ tiên chung lớn nhất của ~x_i~ và ~y_i~.

Sample 1

Input

3 5 0
1 2 6
7 10
8 5
6 2
9 10
2 3

Output

1
5
1
6
1

Sample 2

Input

3 5 1
1 2 6
7 10
8 5
6 2
9 10
2 3

Output

1
6
2
1
1

Giải thích test của các ví dụ:

Hình vẽ cây của cả ~2~ ví dụ chính là hình vẽ ở đầu bài.

Nhãn của các đỉnh trong các truy vấn ở ví dụ thứ ~2~ là:

~x_1 = 7, y_1 = 10,~

~x_2 = 9, y_2 = 6,~

~x_3 = 2, y_3 = 8,~

~x_4 = 1, y_4 = 2,~

~x_5 = 3, y_5 = 4~.

Subtask

~9~ test đầu tiên có: ~q = 1, t = 0~

~9~ test tiếp theo có: ~n \leq 1000, t = 0~

~9~ test tiếp theo có: ~t = 0~

~9~ test cuối cùng có: ~t = 1~