Với một đồ thị ~G~ có hướng không chu trình, ta gọi một dãy ~C = (c_1, c_2, c_3,...c_n)~ là một dãy có thứ tự bắt đầu từ ~c_1~ và kết thúc ở ~c_n~ nếu ~c_1, c_2, c_3,...c_n~ là những đỉnh phân biệt của ~G~ sao cho tồn tại đường đi từ ~c_1~ đến ~c_2~, đường đi từ ~c_2~ đến ~c_3~, ...và đường đi từ ~c_{n-1}~ đến ~c_n~. Lưu ý rằng giữa hai phần tử kề nhau ~c_i~ và ~c_{i+1}~ của dãy có thứ tự ~C~ không nhất thiết phải có cung trực tiếp mà chỉ cần tồn tại đường đi từ ~c_i~ đến ~c_{i+1}~.

Sau khi định nghĩa dãy có thứ tự ~C = (c_1, c_2, c_3,...c_n)~, ta định nghĩa độ dài của dãy là ~len(C) = n~. Vì vậy, độ dài của một dãy có thứ tự là số lượng đỉnh có trong dãy. Lưu ý rằng dãy có thể có độ dài ~1~ khi chỉ chứa ~1~ đỉnh duy nhất, đỉnh đó sẽ vừa là đỉnh bắt đầu vừa là đỉnh kết thúc của dãy.

Với một dãy có thứ tự ~C = (c_1, c_2, c_3,...c_n)~, ta định nghĩa dấu của dãy là ~sgn(C) = (-1)^{len(C)+1}~. Với mỗi cặp đỉnh ~x~ và ~y~ thuộc ~G~, ta gọi ~S_{x, y}~ là tập hợp (set) của tất cả dãy có thứ tự bắt đầu ở ~x~ và kết thúc ở ~y~.

Cuối cùng, ta định nghĩa độ căng giữa đỉnh ~x~ và ~y~ là ~tns(x, y) = \sum_{C \in S_{x, y}} sgn(C)~. Vì vậy, độ căng giữa đỉnh ~x~ và ~y~ bằng tổng dấu của tất cả các dãy có thứ tự bắt đầu ở ~x~ và kết thúc ở ~y~.

Cho một số nguyên ~K~. Bạn hãy dựng một đồ thị có hướng không chu trình với tối đa ~1000~ đỉnh và tối đa ~1000~ cạnh sao cho ~tns(1, N) = K~. Trong đó, ~N~ là số đỉnh của đồ thị. Các đỉnh của đồ thị phải được đánh số bằng các số nguyên dương từ ~1~ đến ~N~.

Input

Gồm ~1~ dòng chứa ~1~ số nguyên ~K~ ~(|K| \le 10^{18})~.

Output

Dòng thứ nhất ghi số đỉnh và số cạnh của đồ thị được dựng. Gọi ~N~ ~(1 \le N \le 1000)~ là số đỉnh và ~M~ (~0 \le M \le 1000)~ là số cạnh của đồ thị đó.

~M~ dòng tiếp theo, dòng thứ ~i~ ghi hai số nguyên ~X_i~ và ~Y_i~ ~(1 \le X_i, Y_i \le N)~, cho biết cung thứ ~i~ nối từ đỉnh ~X_i~ đến đỉnh ~Y_i~. Mỗi cung chỉ được xuất hiện một lần trong output.

Trị tuyệt đối của độ căng giữa mỗi cặp đỉnh trong đồ thị phải nhỏ hơn hoặc bằng ~2^{80}~.

Nếu tồn tại nhiều đáp án, bạn được phép in ra một đáp án bất kỳ.

Sample Input 1

0

Sample Output 1

6 6
1 4
1 5
4 3
5 3
3 2
2 6

Sample Input 2

1

Sample Output 2

1 0

Sample Input 3

2

Sample Output 3

6 8
1 2
1 3
1 4
1 5
5 4
2 6
3 6
4 6

Subtask

• ~5~ test đầu có ~1 \le K < 500~.
• ~5~ test tiếp theo có ~-300 < K \le 1~.
• ~5~ test tiếp theo có ~|K| < 10000~.
• ~12~ test còn lại không có ràng buộc gì thêm.

Note

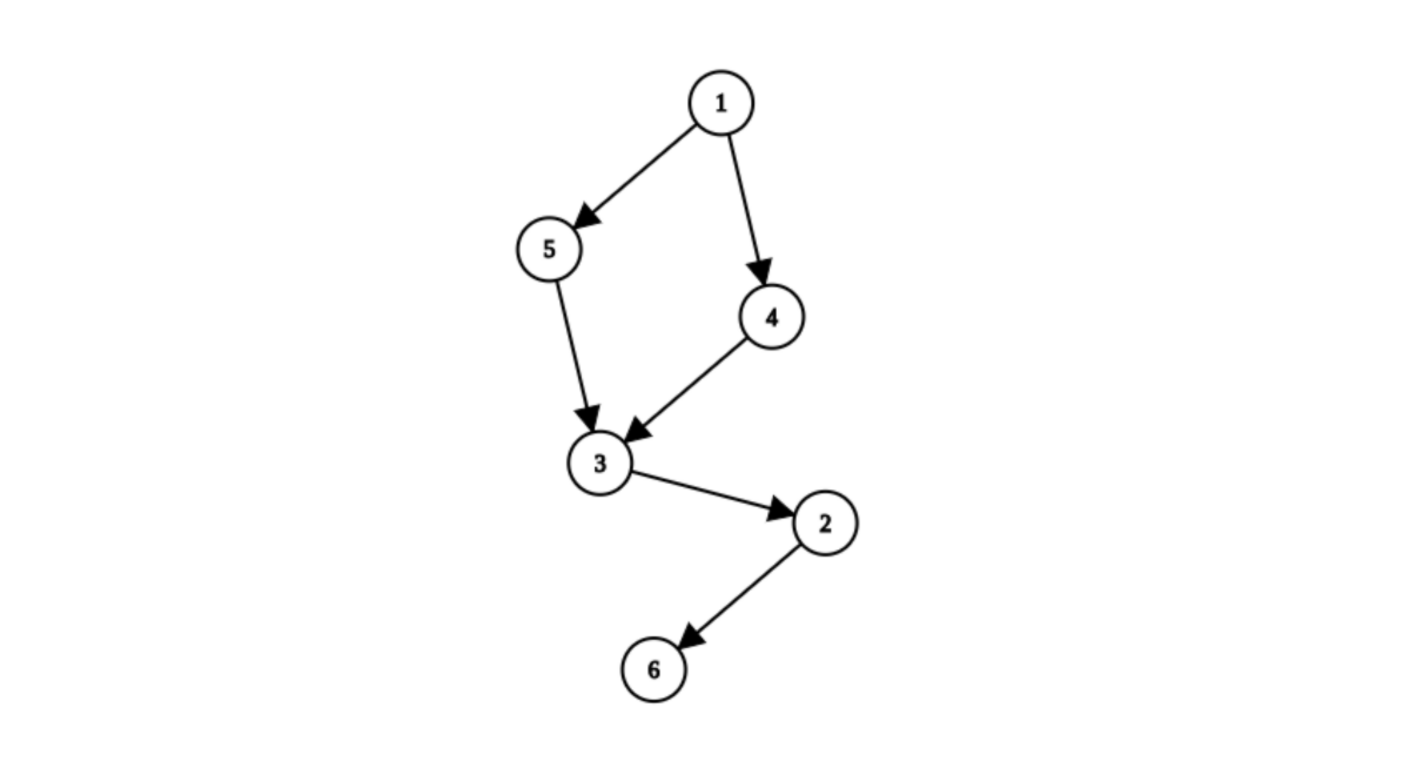
Giải thích ví dụ đầu tiên: Đồ thị được dựng có ~6~ đỉnh. Những dãy có thứ tự bắt đầu ở ~1~ và kết thúc ở ~6~ là: ~(1, 6), (1, 4, 6), (1, 5, 6),~ ~(1, 3, 6),~ ~(1, 2, 6),~ ~(1, 4, 3, 6),~ ~(1, 5, 3, 6),~ ~(1, 5, 2, 6),~ ~(1, 3, 2, 6),~ ~(1, 4, 3, 2, 6),~ ~(1, 5, 3, 2, 6)~. Độ dài của chúng lần lượt là: ~1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4~, nên dấu của chúng là ~−1, 1, 1, 1, 1, −1, −1, −1, −1, −1, 1, 1~. Vì vậy độ căng giữa ~1~ và ~6~ trong đồ thị này bằng ~−1 + 1 + 1 + 1 + 1 − 1 − 1 − 1 − 1 − 1 + 1 + 1 = 0~.