Có thể bạn đã biết đến một cách biểu diễn các chữ số trên một số thiết bị điện tử (đồng hồ, máy tính) sử dụng ~7~ đoạn thẳng. Tuy nhiên, Matej phản đối và cho rằng có thể biểu diễn các chữ số một cách hiệu quả hơn, chỉ sử dụng ~5~ đoạn như hình dưới đây (không nhất thiết là đoạn thẳng).

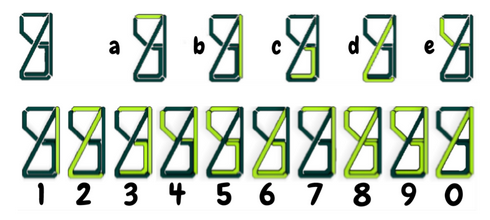
Matej quyết định sẽ khởi nghiệp ở một lĩnh vực rất tiềm năng, bóng đá. Các chữ số được biểu diễn bằng ~5~ đoạn của anh sẽ được sử dụng để thay người trong trận đấu. Bảng thay người gồm ~M~ ô (mỗi ô có ~5~ đoạn), được dùng để hiển thị số áo của cầu thủ rời sân. Ban đầu bảng hiển thị số ~X~. Trong mỗi giây sau đó, Matej sẽ thực hiện một trong hai bước:

• Bật sáng một đoạn đang tắt
• Tắt một đoạn đang bật

Tổng cộng, Matej sẽ làm như vậy ~N~ lần và anh sẽ đảm bảo sau mỗi ~K~ bước thì hiển thị trên bảng phải là một số hợp lệ (những đoạn đang bật sáng tạo ra 1 số hợp lệ). Ngoài ra, những số có ít hơn ~M~ chữ số được cho là hợp lệ nếu chúng chứa số ~0~ dẫn đầu phù hợp.

Với mỗi trạng thái cuối cùng (một số nguyên giữa ~0~ và ~10^M - 1~), Matej muốn biết có bao nhiêu cách để đến được trạng thái cuối cùng này. Hai cách được gọi là khác nhau nếu, giả sử chúng ta thực hiện đồng thời hai cách trên hai bảng khác nhau, thì tồn tại một thời điểm mà trạng thái trên hai bảng khác nhau (Nói cách khác, tồn tại một thời điểm bất kỳ mà khi cầm 2 bảng lên ta thấy các đoạn được bật không giống nhau).

Vì số cách có thể rất lớn, hãy tính theo modulo ~10^9 + 7~

Input

Gồm ~1~ dòng chứa các số nguyên ~M~, ~N~, ~K~ ~(1 \le K \le N)~ và số ~X~ ~(0 \le X \le 10^M)~ .

Output

Dòng thứ ~i~ in ra số cách khác nhau để số ~i - 1~ được hiển thị sau ~N~ bước modulo ~10^9 + 7~

Sample Input 1

1 2 1 5

Sample Output 1

0
0
0
1
0
2
0
0
0
0

Sample Input 2

1 3 3 8

Sample Output 2

0
0
0
6
0
13
0
0
0
0

Sample Input 3

1 4 2 4

Sample Output 3

24
0
8
0
37
0
4
28
4
24

Giải thích Sample test 1: Bảng chỉ gồm duy nhất ~1~ ô để hiển thị ~1~ chữ số, ban đầu hiển thị chữ số ~5~. Sau mỗi bước đi ~(K = 1)~, bảng luôn phải hiển thị một số hợp lệ. Matej sẽ thực hiện ~N = 2~ bước. Vì vậy, sau ~N~ bước, bảng có thể hiện số ~3~ hoặc số ~5~. Số ~3~ chỉ có ~1~ cách để tạo ra ~(5 - 9 - 3)~ và số ~5~ có 2 cách ~(5 - 9 - 5)~ và ~(5 - 8 - 5)~

Subtask

• ~10~ test đầu có ~M = 1, 1 \le N \le 12~
• ~12~ test tiếp theo có ~M = 1, 1 \le N \le 10^{15}~
• ~9~ test tiếp theo có ~M = 2, 1 \le N \le 1500, K = N~
• ~13~ test tiếp theo có ~M = 2, 1 \le N \le 10^{15}, 1 \le K \le 15~
• ~15~ test tiếp theo có ~M = 2, 1 \le N \le 10^{15}, 1 \le K \le 1500~
• ~15~ test tiếp theo có ~M = 2, 1 \le N \le 10^{15} ~