Finding a Centroid
Xem dạng PDFBạn được cho ~1~ cây gồm ~n~ đỉnh. Việc của bạn là tìm ~\texttt{centroid}~ của cây, đỉnh mà nếu lấy nó là gốc của cây, mọi cây con đều có kích thước không quá ~\lfloor \frac{n}{2} \rfloor~.
Input
Dòng đầu chứa số nguyên ~n~ (~1 \le n \le 2 \times 10^5~), số lượng đỉnh của cây. Các đỉnh được đánh số lần lượt từ ~1~, ~2~, ~3~, ~\cdots~, ~n~.
Sau đó là ~n - 1~ dòng là các cạnh của cây. Mỗi dòng gồm ~2~ số nguyên ~a~ và ~b~ (~1 \le a, b \le n~) tương ứng là cạnh giữa ~2~ đỉnh ~a~ và ~b~ trên cây.
Output
In ra chỉ số đỉnh của ~\texttt{centroid}~ của cây. Nếu có nhiều đỉnh thoả mãn thì có thể in đỉnh bất kỳ.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| ~1~ | ~50\%~ | ~1 \leq n \leq 5 \times 10^3~ |
| ~2~ | ~50\%~ | Không có ràng buộc gì thêm |
Sample Input 1
7
1 2
2 3
3 4
3 5
2 6
6 7
Sample Output 1
2
Sample Input 2
10
4 1
6 5
7 2
6 3
1 7
2 10
10 9
3 8
8 9
Sample Output 2
10
Notes
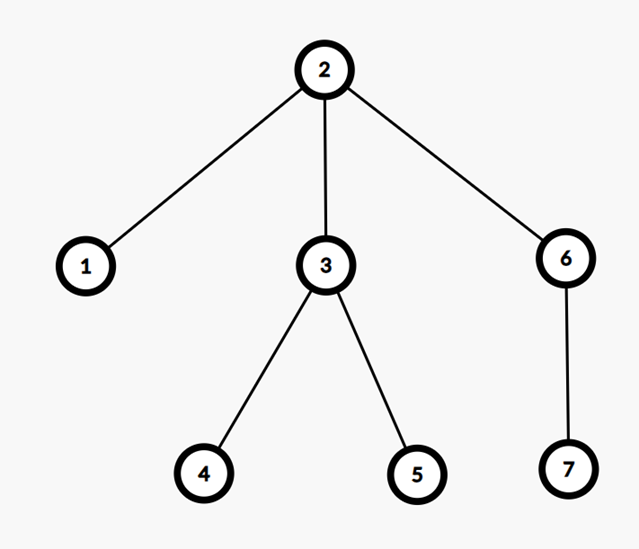
Trong test ví dụ đầu tiên, đỉnh ~2~ là ~\texttt{centroid}~ của cây bởi:
Lấy đỉnh ~2~ là gốc của cây:
— Những cây con có kích thước là ~1~: ~1~, ~4~, ~5~, ~7~.
— Những cây con có kích thước là ~2~: ~6~.
— Những cây con có kích thước là ~3~: ~3~.
Mọi cây con đều có kích thước không quá ~\lfloor \frac{n}{2} \rfloor = \lfloor \frac{6}{2} \rfloor = 3~.

Bình luận
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.