Khi nào thì ~t_i = t_j~?

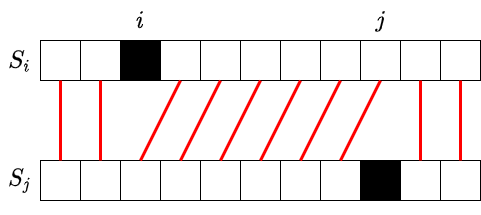
Dựa vào hình vẽ trên, ta thấy:

• Với ~1 \le p < i~, ta có: ~t_i[p] = t_j[p] = s[p]~.
• Với ~i \le k < j~, ta có: ~t_i[p] = s[p + 1]~, ~t_j[p] = s[p]~.
• Với ~j \le p < n~, ta có: ~t_i[p] = t_j[p] = s[p + 1]~.

Vì vậy, ~t_i = t_j~ khi và chỉ khi ~s[i] = s[i + 1] = \ldots = s[j]~.

Để đếm số cặp số ~(i, j)~ thỏa điều kiện này, có rất nhiều cách khác nhau: ta có thể tách xâu ~s~ ban đầu thành các đoạn liên tiếp có ký tự giống nhau. Với một đoạn ký tự độ dài ~k~, ta sẽ tìm được ~\frac{k(k - 1)}{2}~ cặp số ~(i, j)~ thỏa mãn.

Độ phức tạp: ~O(|s|)~.

Code mẫu

#include <bits/stdc++.h>
using namespace std;

void solve() {
    int n;
    cin >> n;
    string s;
    cin >> s;
    long long ans = 0;
    for (int i = 0, j = 0; i < n; i = j) {
        while (j < n && s[i] == s[j])
            j++;
        ans += 1LL * (j - i) * (j - i - 1) / 2;
    }
    cout << ans << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    solve();
}