Nhận xét: Xem mỗi ô trong mê cung là ~1~ đỉnh của đồ thị, với mỗi ô ~(i, j)~ chúng ta xây cạnh đến các ô mà từ ~(i, j)~ có thể đến trong ~1~ bước di chuyển. Nếu đồ thị mà mọi cạnh có chung trọng số thì có thể sử dụng thuật toán BFS để tìm đường đi ngắn nhất giữa ~2~ đỉnh, dễ thấy đồ thị trong bài thỏa mãn điều kiện trên với trọng số chung là ~1~. Vậy ta chỉ cần dựng được đồ thị thì có thể giải quyết được bài toán.

Tuy nhiên, độ phức tạp của thuật toán BFS là ~O(n+m)~ với đồ thị ~n~ đỉnh ~m~ cạnh dẫn đến chúng ta cần chứng minh rằng số cạnh đủ nhỏ để chạy BFS trong ~1~ giây. Nếu bạn không tỉnh táo sẽ bị vướng ở bước này.

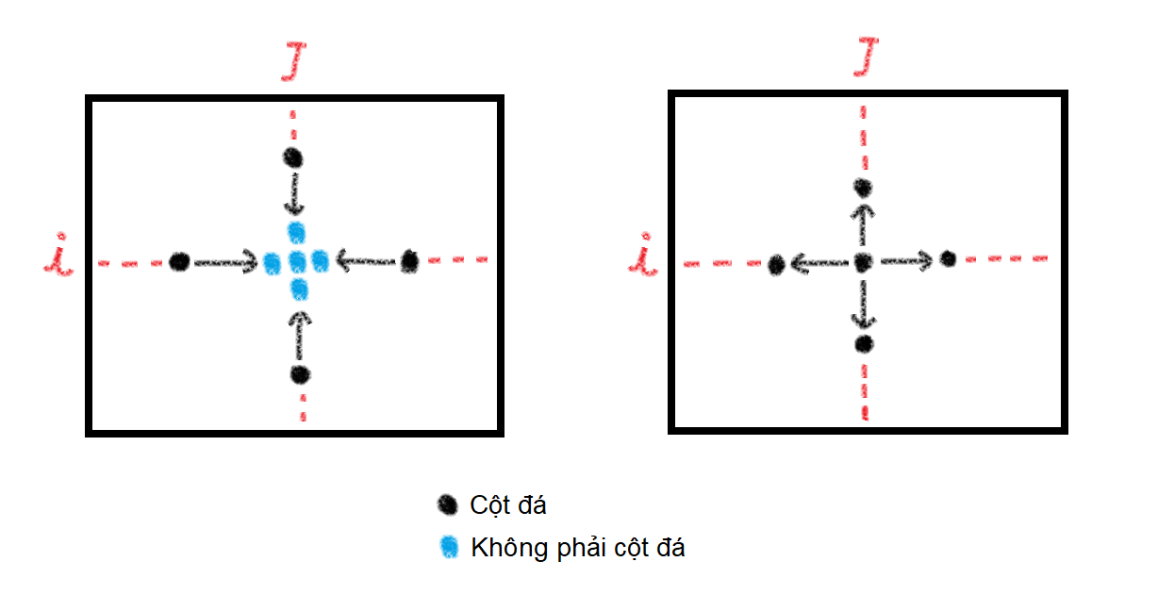
Chứng minh số cạnh trên đồ thị ~\leq~ ~8\times N \times M~:

• Nếu ô ~(i, j)~ không phải cột đá thì có tối đa:

~4~ cạnh từ các cột đá gần nhất ở mỗi hướng Đông Tây Nam Bắc đến ô ~(i, j)~

~4~ cạnh từ ~(i, j)~ đến các ô ~(i−1, j), (i, j+1), (i+1, j), (i, j−1)~

• Nếu ô ~(i, j)~ là cột đá thì có tối đa:

~4~ cạnh từ ô ~(i, j)~ đến các cột đá gần nhất ở mỗi hướng Đông Tây Nam Bắc

• Do mê cung gồm ~N \times M~ ô thuộc ~2~ trường hợp trên, hiển nhiên đồ thị có không quá ~8 \times N \times M~ cạnh

Code mẫu

#include <bits/stdc++.h>
using namespace std;

#define int ll
#define vt vector
#define TASK ""
#define pb push_back
#define all(x) begin(x), end(x)
#define sz(x) (int)(x).size()
#define f first
#define s second
#define MASK(i) (1ll << (i))
#define BIT(x, i) (((x) >> (i)) & 1ll)
#define builtin_popcount __builtin_popcountll
#define Times cerr <<"\nTime: "<<clock()/(double)1000<<" sec"
// cout << setprecision(0) << fixed << ans;

#define FOR(i, l, r) for (int i = (l); i <= (r); ++i)
#define rep(i, r, l) for (int i = (r); i >= (l); --i)
// Dang Quoc Cuong 196 147 :>>

typedef long long ll;
typedef pair<int,int> ii;
typedef pair<int, ii> iii;
const int INF = 1e9;
const int mod = 1e9 + 7;
const int N = 2e3 + 5;
const int Sz = 1e6 + 5;
const int dx[] = {1, 0, -1, 0};
const int dy[] = {0, -1, 0, 1};

void setIO() {
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    if (fopen(TASK".inp","r")) {
        freopen(TASK".inp","r",stdin);
        freopen(TASK".out","w",stdout);
    }
}
/***------------------------- END ---------------------------***/
int n, m, a[N][N], dis[N][N], ans, k;
queue<ii> Q;

bool inside(int x, int y) {
    return x >= 1 && x <= n && y >= 1 && y <= m;
}

void add(int u, int v, int x, int y) {
    if (inside(x, y) && dis[x][y] == 0) {
        dis[x][y] = dis[u][v] + 1;
        Q.push(ii(x, y));
    }
}

void bfs() {
    Q.push(ii(1, 1));
    dis[1][1] = 1;

    while (sz(Q)) {
        ii u = Q.front();
        Q.pop();

        if (u == ii(n, m)) {
            ans = dis[n][m] - 1;
            return;
        }

        if (!a[u.f][u.s]) {
            FOR(i, 0, 3) {
                int vx = u.f + dx[i], vy = u.s + dy[i];
                add(u.f, u.s, vx, vy);
            }
        }
        else {
            FOR(i, 0, 3) {
                FOR(j, 1, k) {
                    int vx = u.f + dx[i]*j, vy = u.s + dy[i]*j;
                    add(u.f, u.s, vx, vy);
                    if (a[vx][vy]) break; 
                }
            }
        }
    }
}

void test_case() {
    cin >> n >> m;
    k = max(n, m);

    FOR(i, 1, n) FOR(j, 1, m) cin >> a[i][j];

    bfs();

    cout << ans;
}

signed main() {
    setIO();
    int TC = 1;

    while (TC--) {
          test_case();
    }
    return 0;
}
/*** quoccuong ***/