Giả sử ban đầu dãy không có phần tử nào, ta sẽ điền dần các phần tử vào mảng theo thứ tự tăng dần về giá trị.

Khi đó sau mỗi lần thêm phần tử, các đoạn với ~k~ vị trí chưa được điền vào có giá trị bằng tổng của các phần tử trong đoạn ngay lúc đó.

Vậy tại mỗi lần duyệt, ta sẽ cập nhật lại đáp án bằng max của các đoạn có đúng ~k~ phần tử chưa được đánh dấu.

Đặt ~r_l=~ chỉ số nhỏ nhất thỏa mãn đoạn ~[l, r_l]~ có đúng ~k~ phần tử chưa được đánh dấu. Giá trị của một đoạn chứa đúng ~k~ phần tử chưa được đánh dấu sẽ là (tổng các phần tử được đánh dấu trong đoạn) + (tổng suffix lớn nhất kết thúc tại ~l-1~) + (tổng prefix lớn nhất bắt đầu tại ~r_l+1~).

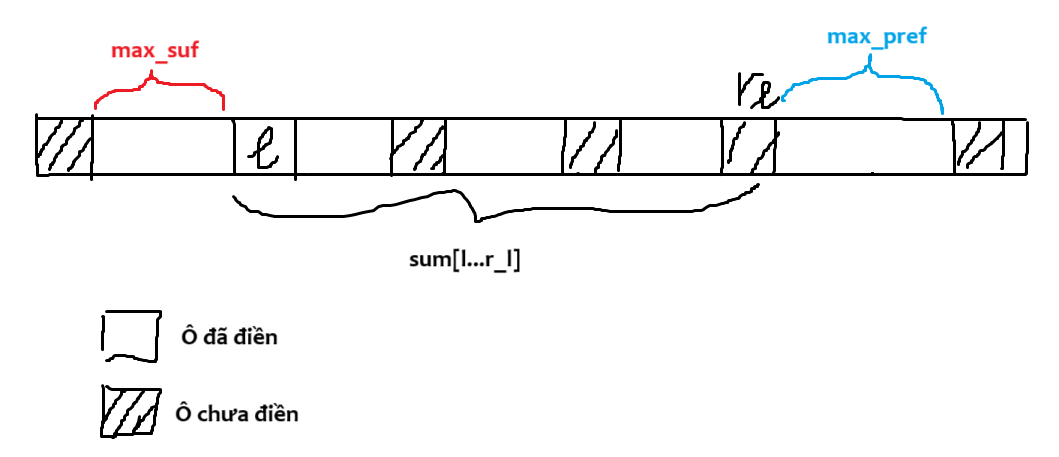
Dễ thấy, đáp án chỉ phụ thuộc vào các đoạn ~[l, r_l]~ mà ô ~l~ chưa được điền. Tức là ta chỉ cập nhật đáp án với giá trị của các đoạn có dạng ~[l, r_l]~ với ô ~l~ chưa điền.

Đồng thời, khi ta đánh dấu một phần tử mới, chỉ có tối đa ~k~ vị trí ~l~ mà:

• ~r_l~ bị thay đổi.
• Ô thứ ~l~ chưa được điền

~\Rightarrow~ Ta duyệt lại tất cả các giá trị ~l~ thỏa mãn, tổng số lần duyệt là ~n\times k~.

Code mẫu:

#include <bits/stdc++.h>
using namespace std;

const int N = 3e5 + 3;
int n, k;
int a[N], prv[N], nxt[N];
pair<int, int> b[N];
long long prf[N];
long long max_prf[N], max_suf[N];

int main() {
  freopen("maxsub.inp", "r", stdin);
  freopen("maxsub.out", "w", stdout);
  cin >> n >> k;
  for (int i = 1; i <= n; ++i) {
    cin >> a[i];
    b[i] = {a[i], i};
    prf[i] = prf[i - 1] + a[i];
    prv[i] = i - 1, nxt[i] = i + 1;
  }

  if (k == 0) {
    long long ans = 0, mn = 0;
    for (int i = 1; i <= n; ++i) {
      ans = max(ans, prf[i] - mn);
      mn = min(mn, prf[i]);
    }
    return cout << ans << '\n', 0;
  }

  sort(b + 1, b + n + 1);
  long long ans = 0;
  for (int i = 1; i <= n - k; ++i) {
    auto [val, id] = b[i];
    int l = id;
    for (int j = 0; j < k; ++j) {
      if (!prv[l]) break;
      l = prv[l];
    } 
    int r = l;
    long long sum = a[l];
    for (int j = 0; j < k; ++j) {
      r = nxt[r];
      sum += a[r];
    }
    sum -= a[id];

    while (l != nxt[id] && r != n + 1) {
      ans = max(ans, prf[r] - prf[l - 1] - sum + max_suf[l] + max_prf[r]);
      sum -= a[l];
      l = nxt[l], r = nxt[r];
      if (r != n + 1) {
        sum += a[r];
      }
    }

    if (prv[id]) {
      int t = prv[id];
      max_prf[t] = max(max_prf[t], prf[id] - prf[t] + max_prf[id]);
    }

    if (nxt[id] != n + 1) {
      int t = nxt[id];
      max_suf[t] = max(max_suf[t], prf[t - 1] - prf[id - 1] + max_suf[id]);
    }

    nxt[prv[id]] = nxt[id];
    prv[nxt[id]] = prv[id];
  }
  cout << ans << '\n';
}