Bedao OI Contest 1 - Đếm cầu
Xem dạng PDF
Quân có đồ thị vô hướng, liên thông ~n~ đỉnh, ~m~ cạnh. Quân cần xử lý ~q~ truy vấn có dạng sau:
- ~A\ B\ C\ D~: Thêm cạnh ~A - B~, cho biết, đồ thị mới có bao nhiêu cạnh là cầu nằm trên bất kỳ đường đi đơn nào đi từ ~C \rightarrow D~.
Biết rằng, các truy vấn độc lập với nhau (Tức là cạnh được thêm vào chỉ tồn tại cho đến hết truy vấn đó).
Nhắc lại: Một cạnh được gọi là cầu nếu xóa cạnh đó thì số miền liên thông tăng lên.
Input
Dữ liệu vào từ file văn bản bridge.inp
Dòng đầu gồm ba số nguyên dương ~n, m, q~ lần lượt là số đỉnh, số cạnh của đồ thị và số truy vấn cần xử lý (~1 \le n, m, q \le 10^5~).
~m~ dòng tiếp theo, mỗi dòng gồm hai số ~u, v~ biểu diễn cạnh ~u - v~ trên đồ thị (~1 \le u, v \le n~).
~q~ dòng tiếp theo, mỗi dòng gồm bốn số ~A, B, C, D~, biểu diễn một truy vấn có dạng ~A\ B\ C\ D~ (~1 \le A, B, C, D \le n~).
Output
Kết quả in ra file văn bản bridge.out
In ra ~q~ dòng tương ứng với câu trả lời cho ~q~ truy vấn.
Scoring
| Subtask | % số test | Giới hạn |
|---|---|---|
| 1 | ~20\%~ | ~n,m,q \le 100~ |
| 2 | ~25\%~ | ~n,m,q \le 5000~ |
| 3 | ~25\%~ | ~m = n - 1~ |
| 4 | ~30\%~ | Không có điều kiện gì thêm. |
Sample Input 1
6 6 2
1 3
2 3
1 2
3 5
3 6
1 4
4 6 4 5
4 6 1 2
Sample Output 1
1
0
Notes
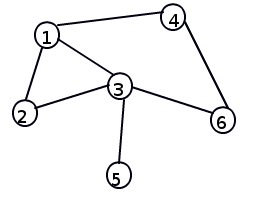
Trong cả ~2~ truy vấn, ta chỉ thêm cạnh ~4 - 6~. Sau khi thêm cạnh ~4 - 6~, đồ thị sẽ như trên.
Trong truy vấn ~1~, các đường đi từ ~4 \rightarrow 5~ bao gồm:
~4 \rightarrow 6 \rightarrow 3 \rightarrow 5~
~4 \rightarrow 1 \rightarrow 3 \rightarrow 5~
~4 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 5~
Ta thấy cạnh ~3 - 5~ là cầu, và nằm trên đường đi từ ~4 \rightarrow 5~. Vì chỉ có cạnh ~3 - 5~ là cầu, đáp án là ~1~.
Trong truy vấn ~2~, không có cầu nào nằm trên đường đi từ ~1 \rightarrow 2~. Vì vậy, đáp án là ~0~.
Bình luận
.
Dành cho các bạn đang bị WA với 36/40:
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.