Subtask 1: ~N \leq 10^6~

For this subtask, we can check all numbers from ~1~ to ~N~ to see which ones are both divisors of ~N~ and divisible by at least two of the three numbers ~A, B, C~.

Complexity: ~O(N)~.

Subtask 2: ~N \leq 10^{12}~

We will try to reduce the complexity by finding all positive divisors of ~N~ within ~\sqrt{N}~. You can read more about it here.

Complexity: ~O(\sqrt{N})~.

Subtask 3: ~N \leq 10^{18}~ and ~A,B,C \geq 10^{6}~

Before diving into the analysis, we will make two small observations:

• Observation 1: If a positive integer ~k~ is a divisor of the number ~n~ and ~k~ is divisible by ~x~, then ~n~ is also divisible by ~x~.

• Observation 2: The positive integer ~n~ is divisible by two positive integers ~A~ and ~B~ if and only if ~n~ is divisible by the Least Common Multiple of ~A~ and ~B~.

To find the number of divisors divisible by ~2~ out of ~3~, we will apply inclusion-exclusion. Let ~f(X)~ be the number of divisors of ~N~ that are divisible by ~X~.

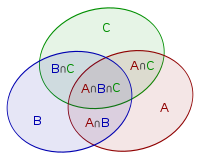
From the Venn diagram and Observation 2, it is easy to derive the formula ~f[LCM(A,B)] + f[LCM(B,C)] + f[LCM(C,A)] - 2 \times f[LCM(A,B,C)]~.

Finally, how to find ~f(X)~ with ~N \leq 10^{18}~? If there does not exist any integer ~k~ such that ~N = k\cdot X~, then ~f(X) = 0~. Conversely, we will have ~N = k\cdot a\cdot X~ where ~k~ is an integer and ~a~ is a divisor of ~N~. Thus, we only need to count the number of satisfying ~a = \frac{N}{kX}~, or in other words, find the number of divisors of ~\frac{N}{X}~.

Note that when finding ~LCM(A,B)~, we need to check if that number exceeds ~N~ to avoid overflow.

Complexity: ~O(\sqrt{\frac{N}{X}}) \sim O(\sqrt{10^{12}}) = O(10^6)~ with ~X \sim \min(A,B,C)~.

#include<iostream>
#include<stdio.h>

using namespace std;


long long A,B,C,N;
long long AB, BC, CA, ABC;
long long res = 0;

long long GCD(long long a,long long b)
{
    long long r;
    while(b != 0)
    {
        r = a%b;
        a = b;
        b = r;
    }
    return a;
}

// LCM(a,b) = a*b/GCD(a,b) <= n
// => b/GCD(a,b) <= n/a

long long LCM(long long a,long long b)
{
    if(a == -1 || b == -1)
        return -1;
    long long g = GCD(a,b);

    // Nếu LCM(a,b) > N thì bỏ qua
    if(b/g > N/a)
        return -1;

    return (a/g)*b;
}

long long solve(long long N,long long q)
{ 
    if(q == -1)
        return 0;
    if(N%q != 0)
        return 0;

    long long n = N/q;
    long long res = 0;
    for(long long i = 1;i*i <= n;i++)
        if(n%i == 0) {
            if(i*i == n)
                res++;
            else
                res += 2;
        }
    return res;
}

int main()
{

    cin >> N >> A >> B >> C;

    AB = LCM(A,B);
    BC = LCM(B,C);
    CA = LCM(C,A);
    ABC = LCM(LCM(A,B),C);

    res = solve(N,AB) + solve(N,BC) + solve(N,CA) - 2*solve(N,ABC);

    cout << res;

}