Bedao Mini Contest 17 - PLUS
Xem dạng PDFCho một ma trận ~a~ kích thước ~n \times m~, tìm hai dấu cộng không có điểm chung trên ma trận sao cho tổng giá trị nằm trên hai dấu cộng là lớn nhất.
Một dấu cộng là hai đoạn thẳng có độ dài lẻ và bằng nhau, một đoạn thẳng nằm ngang, một đoạn thẳng nằm dọc và giao nhau tại trung điểm.
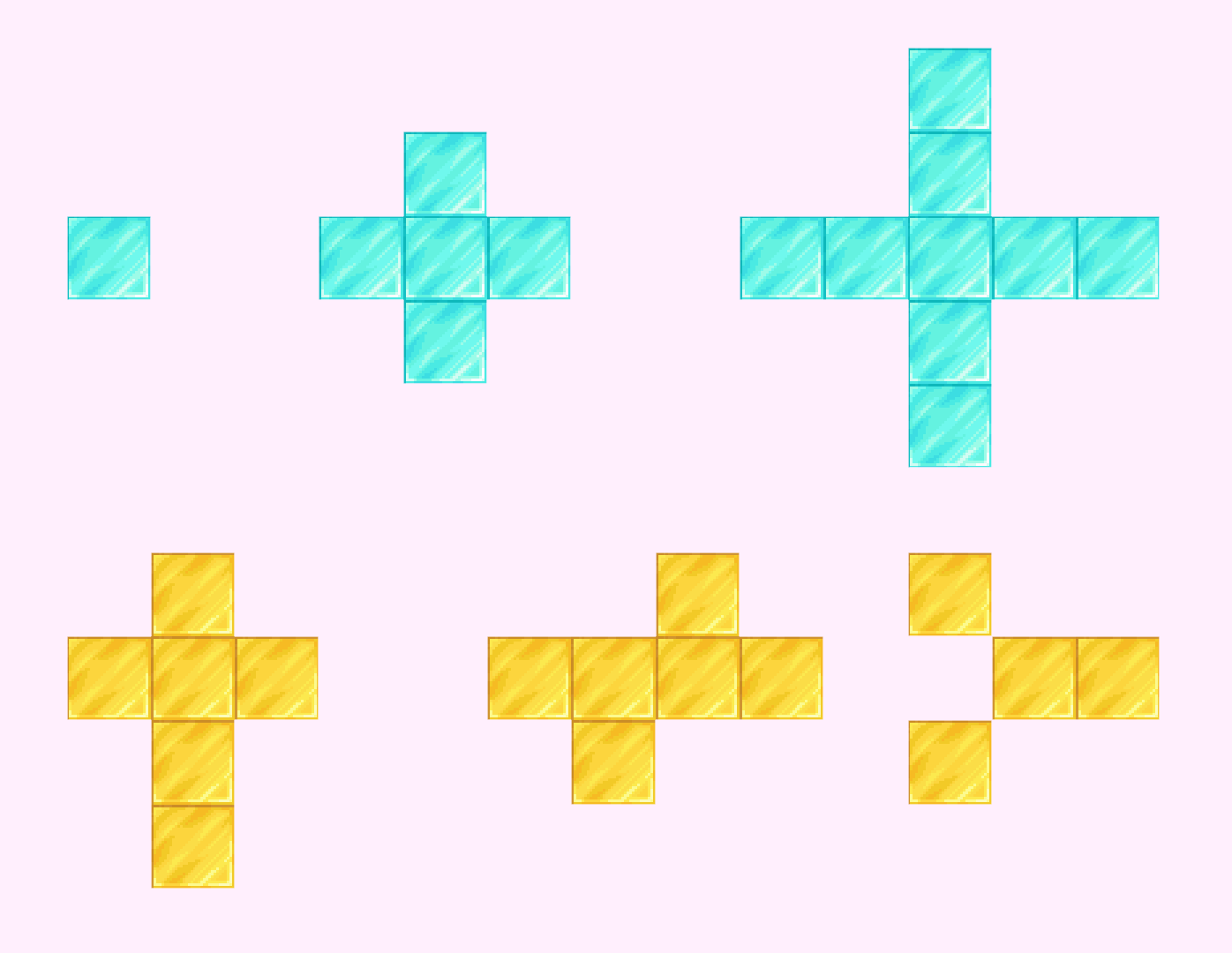
Ảnh ví dụ.
Các hình màu xanh là dấu cộng, màu vàng không phải là dấu cộng.
Input
Dòng đầu tiên chứa hai số nguyên ~n~ và ~m~ lần lượt là số hàng và số cột của ma trận ~a~ ~(2 \le n, m \le 15)~
Trên ~n~ dòng sau, dòng thứ ~i~ chứa ~m~ số nguyên, số thứ ~j~ miêu tả ~a_{ij}~, giá trị của ô hàng ~i~ cột ~j~ ~(-10^6 \le a_{ij} \le 10^6)~
Output
- In ra trên một dòng một số nguyên duy nhất là kết quả của bài toán.
Subtask
~30\%~ số test có ~n, m \leq 3~.
~70\%~ số test còn lại không có ràng buộc gì thêm.
Sample Input 1
3 3
2 1 1
1 2 1
1 -1 -1
Sample Output 1
6
Note
Chọn hai dấu cộng sau:
Dấu cộng thứ nhất có tâm ở đỉnh ~(2,2)~ và có độ lớn là ~3~ (độ lớn ở đây là độ dài của ~2~ đoạn thẳng trong dấu cộng đó). Tổng các phần tử nằm trong dấu cộng này là ~2+1+1+1+(-1)=4~.
Dấu cộng thứ hai có tâm ở đỉnh ~(1,1)~ và có độ lớn là ~1~. Tổng các phần tử nằm trong dấu cộng này là ~2~.
Từ đó tổng tất cả các phần tử khi chọn cả ~2~ dấu cộng trên là ~4+2=6~. Có thể thấy được không có cách để chọn ~2~ dấu cộng ra tổng lớn hơn trong trường hợp trên.

Bình luận