Subtask 1 : ~(q = 1, n \times m \leq 10^6)~

Bài toán cần giải quyết trong subtask : Cho ~1~ bảng hình chữ nhật kích cỡ ~n \times m~, hỏi có bao nhiêu đường đi từ góc trái trên xuống góc phải dưới của bảng mà không đi qua các ô bị cấm ?

Đây là bài quy hoạch động cơ bản, bạn có thể đặt ~F(i, j)~ là số đường đi từ góc trái trên đến ô có tọa độ ~(i, j)~ trong bảng, công thức truy hồi sẽ là :

• ~F(i, j) = 0~ nếu ~(i, j)~ là ô bị cấm.
• ~F(i, j) = F(i-1, j) + F(i, j-1)~ vì để đi đến ô ~(i, j)~ thì cần đi qua ô ~(i-1, j)~ hoặc ~(i, j-1)~.

Subtask 2 : ~(q = 1, x < 0)~

Bạn có thể tham khảo một bài toán tương tự với subtask 2: Link

Subtask 3 :

Đầu tiên bạn cần giải quyết bài toán đếm số đường đi giữa ~2~ điểm trên mặt phẳng mà khoảng cách Manhattan của chúng bé hơn hoặc bằng ~2 \times 10^6~. Đây là bài cơ bản và bạn có thể đọc về nó tại VNOI Wiki - Số học 5

Nhận xét 1: Vùng liên thông chứa các ô bị cháy luôn có dạng hình vuông với góc trái dưới là ~(x-t, x-t)~ và góc phải trên là ~(x+t, x+t)~

Nhận xét 2: Giả sử hình vuông chứa các ô bị cháy nằm gọn trong hình chữ nhật có góc trái trên ~(0, a)~ và góc phải dưới ~(b, 0)~. Nếu ~1~ con đường đi từ ~A~ đến ~B~ và đi qua ít nhất ~1~ ô bị cháy thì con đường đó chắc chắc phải đi qua ~1~ ô thuộc đường chéo phụ của hình vuông trên ( tham khảo hình bên dưới ).

Dễ thấy trong trường hợp tổng quát ( hình vuông chứa các ô bị cháy có thể không hoàn toàn nằm trong hình chữ nhật ), Nhận xét 2 vẫn đúng. Mặt khác, mọi ô thuộc đường chéo phụ phải nằm thẳng hàng với ~2~ điểm ~(x-t, x-t)~ và ~(x+t, x+t)~, có nghĩa tọa độ của chúng luôn có dạng ~(i, i)~

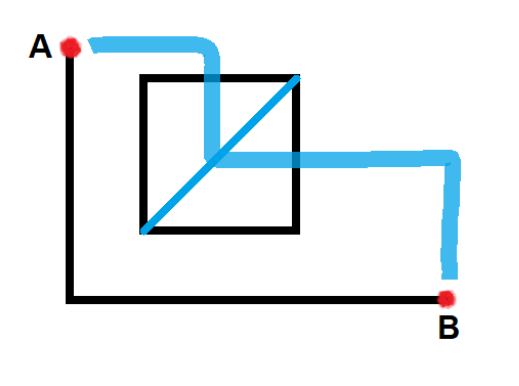
Từ các nhận xét trên, dễ thấy với mỗi truy vấn ta không nhất thiết phải xét hết mọi ô bị cháy mà chỉ cần xét các ô có tọa độ dạng ~(i, i)~. Mỗi truy vấn trong bài được viết lại như sau : Cho ~1~ cặp số ~x-t~ và ~x+t~, hỏi có bao nhiêu đường đi mà trên đó không tồn tại ô có tọa độ ~(i, i)~ thỏa mãn ~x-t \leq i \leq x+t~.

Vậy với mọi ô có tọa độ ~(i, i)~ thỏa mãn ~0 \leq i \leq min(a, b)~, ta đếm số đường đi có dạng ~A → (i, i) → B~ rồi lưu vào Prefix sum để trả lời các truy vấn.

Lưu ý: Vì trong bài này ~x-t~ và ~x+t~ có thể âm hoặc rất lớn nên khi cài đặt thuật toán hãy cẩn thận để tránh lỗi.

Code mẫu

#include <bits/stdc++.h>
using namespace std;

const int N = 2e6 + 10;
const int MOD = 1e9 + 7;

int a, b, q;
int fact[N], inv[N], pre[N], suf[N];

int powmod(int n, int k) {
    if (k == 0) {
        return 1;
    }
    int res = powmod(n, k >> 1);
    res = 1ll * res * res % MOD;
    if (k & 1) {
        res = 1ll * res * n % MOD;
    }
    return res;
}

int nCk(int n, int k) {
    assert(n >= k);
    return 1ll * fact[n] * inv[k] % MOD * inv[n - k] % MOD;
}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cin >> a >> b >> q;
    fact[0] = 1;
    for (int i = 1; i < N; ++i) {
        fact[i] = 1ll * fact[i - 1] * i % MOD;
    }
    inv[N - 1] = powmod(fact[N - 1], MOD - 2);
    for (int i = N - 2; i >= 0; --i) {
        inv[i] = 1ll * inv[i + 1] * (i + 1) % MOD;
    }
    assert(inv[0] == 1);
    int n = min(a, b);
    for (int i = 0; i <= min(a, b); ++i) {
        pre[i] = suf[i] = 1ll * nCk(a, i) * nCk(b, i) % MOD;
    }
    for (int i = 1; i <= n; ++i) {
        pre[i] = (pre[i] + pre[i - 1]) % MOD;
    }
    for (int i = n - 1; i >= 0; --i) {
        suf[i] = (suf[i] + suf[i + 1]) % MOD;
    }

    while (q--) {
        int x, t;
        cin >> x >> t;
        int l = max(0, x - t);
        int r = min(n, x + t);
        if (l > r) {
            cout << nCk(a + b, a) << '\n';
        } else {
            int res = 0;
            if (l > 0) {
                res = (res + pre[l - 1]) % MOD;
            }
            if (r < n) {
                res = (res + suf[r + 1]) % MOD;
            }
            cout << res << '\n';
        }
    }

    return 0;
}