Subtask 1 : ~x = 1~

Dễ thấy mọi con đường đều có ~GCD = 1~ vì chúng luôn xuất phát ở ô ~(x, x)~ có giá trị bằng ~1~, tổng ~GCD~ trong trường hợp này chính là số con đường có thể đi từ ô ~(1, 1)~ tới ô ~(n, m)~.

Note: Tham khảo mục Hệ số nhị thức (Binomial Coefficients) của bài viết sau nếu bạn chưa biết cách tính số đường đi từ ô ~(1, 1)~ tới ô ~(n, m)~ tại: Số học 5 - Các kiến thức cơ bản về Tổ hợp (Combinatorics)

Subtask 2 : ~t \leq 5~

Một số corner case cần lưu ý:

• Nếu ~n = 1~ và ~m = 1~, đáp án hiển nhiên là ~x \times x~.
• Nếu ~1~ trong ~2~ chiều ~n~ hoặc ~m~ bằng ~1~, đáp án là ~x~.

(sử dụng thuật toán bên dưới cho 2 case này sẽ gây lỗi)

Nhận xét #1: Chọn ~1~ số nguyên dương ~d~ bất kỳ, tô mọi ô ~(i, j)~ có giá trị ~i \times j~ chia hết cho ~d~ bằng màu đen và những ô còn lại bằng màu trắng. Nếu ô ~(i, j)~ là ô đen nhưng ~i, j~ đều không chia hết cho ~d~ thì các ô chung cạnh với nó sẽ là ô trắng (Phản chứng : ~2~ giá trị cùng chia hết cho ~d~ thì chênh lệch giữa chúng phải chia hết cho ~d~, tức ~\neq~ ~i, j~), ta gọi các ô đen có đặc điểm như trên là bị cô lập.

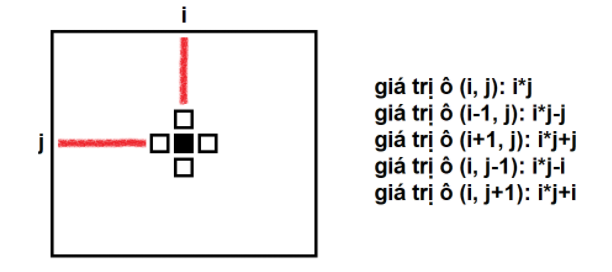
Nhận xét #2: Giả sử có ít nhất ~1~ con đường có ~GCD = d~ ~\rightarrow~ tồn tại con đường đi từ ô ~(x, x)~ tới ô ~(x+n-1, x+m-1)~ mà chỉ đi qua các ô đen ~\rightarrow~ hiển nhiên ô ~(x, x)~ và ~(x+n-1, x+m-1)~ là các ô đen không bị cô lập ~\rightarrow~ ~d~ là ước chung của ~x~ và ~x+n-1~ hoặc ~x~ và ~x+m-1~.

Nhận xét #3: Nếu ~2~ số nguyên dương ~a, b~ có ~1 \leq |a-b| ≤ 5 \times 10^5~ thì ~GCD(a, b) \leq 5 \times 10^5~ vì ~|a-b|~ luôn chia hết cho ~GCD(a, b)~. Thay ~a, b~ bằng ~x~ và ~x+n-1~ (hoặc ~x+m-1~) ~\rightarrow~ ~GCD~ của mọi con đường luôn bé hơn hoặc bằng ~5 \times 10^5~.

Với mỗi số nguyên dương ~d \in [1, 5 \times 10^5]~ cần tính xem bao nhiêu con đường có ~GCD = d~.

Gọi ~f(d)~ là số con đường gồm toàn ô đen nếu số được chọn là ~d~, ~g(d)~ là số con đường có ~GCD = d~, nếu ta tính được ~f(d)~ ~∀~ ~d \in [1, 5 \times 10^5]~ thì cũng sẽ tính được ~g(d)~ ~∀~ ~d \in [1, 5 \times 10^5]~ bằng thuật toán sau:

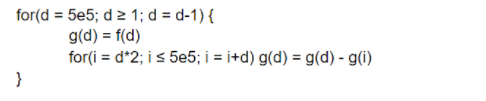
Độ phức tạp của thuật toán trên là: ~O(\sum_{i=1}^{5 \times 10^5} \frac{5 \times 10^5}{i})~ tức ~O(5 \times 10^5 \times log_2(5 \times 10^5))~

Bài toán quay về tính ~f(d)~ ~∀~ ~d \in [1, 5 \times 10^5]:~

• Nếu ~d~ không là ước chung của ~x~ và ~x+n-1~ (hoặc ~x+m-1~) thì ~f(d) = 0~.
• Nếu ~d~ thỏa mãn, ta chỉ quan tâm các ô ~(i, j)~ đen sao cho ~i~ hoặc ~j~ chia hết cho ~d~ (mọi ô đen còn lại đều bị cô lập), dễ thấy chúng tạo thành hình dạng như sau :

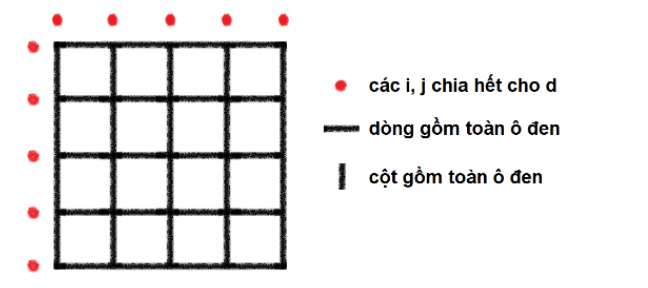
Có thể coi hình dạng đặc biệt này như một bảng ~2~ chiều mới, điều kiện từ mỗi ô được đi sang phải và xuống dưới vẫn giữ nguyên vì vậy ta có thể tính được ~f(d)~ bằng tổ hợp.

Subtask 3:

Nếu ~f(d) = 0~ thì có thể bỏ qua vì chúng không làm ảnh hưởng đến kết quả, vậy ta sẽ lọc ra các trước các số d là ước chung của của ~x~ và ~x+n-1~ (hoặc ~x+m-1~) rồi xếp lại theo thứ tự tự tăng dần.

Sử dụng thuật toán sau để tìm ra ~g(d)~ ~∀~ ~d \in [1, 5 \times 10^5]~ khi biết ~f(d)~ ~∀~ ~d \in [1, 5 \times 10^5]~ (ở đây ~d~ là mảng chứa ước chung đã được lọc ra trong bước trước và ~s~ là kích cỡ của mảng ~d~ tính từ vị trí ~1~):

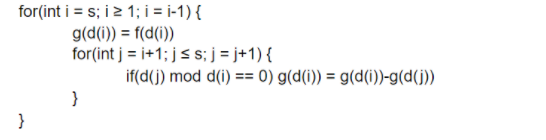
Độ phức tạp của thuật toán trên là: ~O(s^2)~ với mỗi test case, trong thực tế ~s~ lớn nhất chỉ lên tới ~336~ và thuật toán ~O(t \times s^2)~ hoàn toàn đủ nhanh để qua giới hạn thời gian ~1.5s~

Code mẫu

#include <bits/stdc++.h>

using namespace std;

const int MOD = 1e9 + 7;

inline void add(int& a, int b) {
    if ((a += b) >= MOD) a -= MOD;
}

inline void sub(int& a, int b) {
    if ((a -= b) < 0) a += MOD;
}

int binpow(int a, int b) {
    int c = 1;
    while (b) {
        if (b & 1)
            c = (long long)c * a % MOD;
        b >>= 1;
        a = (long long)a * a % MOD;
    }
    return c;
}

vector<int> fact, inv;

void init(int n) {
    fact.resize(n+1); fact[0] = 1; 
    inv.resize(n+1);
    for (int i = 1; i <= n; ++ i) 
        fact[i] = (long long)fact[i-1] * i % MOD;
    inv[n] = binpow(fact[n], MOD - 2);
    for (int i = n; i >= 1; -- i) 
        inv[i-1] = (long long)inv[i] * i % MOD;
}

int ckn(int k, int n) {
    if (k < 0 || k > n) return 0;
    return (long long)fact[n] * inv[k] % MOD * inv[n-k] % MOD;
}

long long x;
int n, m, g[500005];

int calc(int d) {
    if (x % d != 0) return 0;
    if ((x + n - 1) % d != 0 && (x + m - 1) % d != 0) return 0;
    int row = (x + n - 1) / d - x / d, col = (x + m - 1) / d - x / d;
    return ckn(row, row + col);
}

vector<int> get_common_div(long long u, long long v, long long w) {
    vector<int> res;
    int d_v = __gcd(u, v);
    int d_w = __gcd(u, w);
    for (int i = 1; i * i <= max(d_v, d_w); ++ i) {
        if (i * i <= d_v && d_v % i == 0) {
            res.push_back(i);
            res.push_back(d_v/i);
        }
        if (i * i <= d_w && d_w % i == 0) {
            res.push_back(i);
            res.push_back(d_w/i);
        }
    }
    sort(res.begin(), res.end());
    res.resize(unique(res.begin(), res.end()) - res.begin());
    return res;
}

int main() {
    cin.tie(0)->sync_with_stdio(0);
    init(1e6);
    int ntest;
    for (cin >> ntest; ntest --;) {
        cin >> x >> n >> m;
        if (x == 1) {
            cout << ckn(n-1, n+m-2) << "\n";   
        } else {
            // corner case
            if (n == 1 && m == 1) {
                cout << (x % MOD) * (x % MOD) % MOD << "\n";
                continue; 
            } 
            if (n == 1 || m == 1) {
                cout << x % MOD << "\n";
                continue;
            }
            // incl-excl
            int res = 0;
            vector<int> divisors = get_common_div(x, x+m-1, x+n-1);
            for (int j = (int)divisors.size() - 1; j >= 0; -- j) {
                g[j] = calc(divisors[j]);
                for (int i = j + 1; i < (int)divisors.size(); ++ i) 
                    if (divisors[i] % divisors[j] == 0) 
                        sub(g[j], g[i]);
                add(res, (long long)g[j] * divisors[j] % MOD);
            }
            cout << res << "\n";
        }
    }
    return 0;
}